X4L - wzmacniacz z DSP z serii X
Biznes „nagłośnieniowy” – w porównaniu z innymi dziedzinami techniki (np. przemysłem samochodowym, czy ...
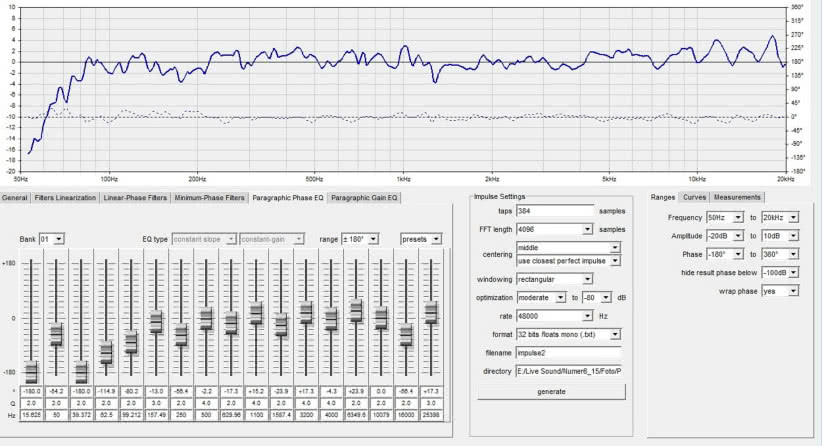
W wakacyjnym numerze poruszyliśmy temat korygowania charakterystyki fazowej, np. zestawów głośnikowych, ale nie tylko. W konkluzji artykułu znalazła się informacja, że znacznie łatwiej niż korzystając z filtrów wszechprzepustowych korygować charakterystykę fazową można za pomocą filtrów FIR. A jak zaprojektować takie filtry?
Nie chodzi tu bynajmniej o projektowanie hardware’owych filtrów, z wykorzystaniem „kości” układów scalonych (procesorów) i mnóstwa innych elementów elektronicznych. To zadanie dla tych, którzy o elektronice nie tylko mają pojęcie „jakie takie”, ale solidnie „siedzą w temacie”. My, zwykli śmiertelnicy, możemy skorzystać z gotowych już urządzeń, które oferują możliwość zaimplementowania zaprojektowanych przez nas filtrów FIR.
W „zamierzchłych” czasach, gdy praktycznie wszystko co było związane z korekcją dźwięku dokonywane było w domenie analogowej, projektowanie filtrów było faktycznie zarezerwowane tylko – jak napisałem wcześniej – dla specjalistów, którzy na tym się dobrze znali. Kto więc chciał skorygować brzmienie jakiegoś urządzenia (np. zestawu głośnikowego) lub dokonać korekcji dźwięku (np. nagłaśnianego czy nagranego instrumentu) musiał skorzystać z gotowych filtrów (w przypadku zwrotnicy zestawu głośnikowego) lub dedykowanych urządzeń, dysponujących zestawem filtrów o regulowanych parametrach (korektorem graficznym, konsoletą z sekcją EQ itp.) W dobie urządzeń cyfrowych zaprojektowanie i wykonanie hardware’u, który będzie odpowiedzialny za korekcję w dalszym ciągu leży po stronie specjalistów w tej dziedzinie, w odróżnieniu jednak od analogowych odpowiedników – które były urządzeniami zaprojektowanymi pod konkretne zastosowania – filtry cyfrowe realizowane są za pomocą urządzeń wielofunkcyjnych, dokonujących skomplikowanych operacji matematyczno-logicznych. Mogą to być stosowane powszechnie procesory DSP, ale również układy programowalne (PLG, FPGA), jak i specjalnie zaprojektowane układy scalone. O ile jednak w analogowym świecie wystarczyło tylko podać na ich wejście sygnał, który chcemy „obrabiać”, aby uzyskać na ich wyjściu sygnał o pożądanych przez nas parametrach, w „cyfrze” jest to bardziej skomplikowane (pomijając już fakt, że układy cyfrowe wymagają sygnału w odpowiednim formacje –cyfrowego, a nie analogowego – a ten może występować w różnych „wariantach”, niekoniecznie kompatybilnych z danym urządzeniem). Rzecz w tym, że takie procesor DSP musi „wiedzieć”, co ma robić, a więc potrzebuje do wykonania danego zadania konkretnych informacji w formie programu. Ale to w dalszym ciągu jeszcze nie wszystko. Oprócz sygnału wejściowego o odpowiednich parametrach i programu, który będzie „sterował” pracą procesora czy innego układu „obrabiającego” cyfrowo nasz sygnał, w przypadku filtracji (a konkretnie filtracji FIR) musimy jeszcze zaprojektować ów filtr, tzn. „poinformować” nasz układ, w jaki sposób ma odfiltrować sygnał wejściowy. I to jest właśnie zadanie dla nas.

Filtr cyfrowy to nic innego jak ciąg liczb (współczynników filtru).
Najpierw jednak w dużym skrócie powiedzmy sobie (lub przypomnijmy, jeśli ktoś już coś na ten temat wie – choćby z artykułów w LSI, w których już ten temat kiedyś poruszaliśmy) co to są w ogóle filtry cyfrowe – ze szczególnym naciskiem na filtr typu FIR – jak działają, czym się cechują i jakie są ich wady i zalety.
W filtrach analogowych wykorzystując właściwości fizyczne takich elementów jak kondensatory, cewki i rezystory w odpowiedni sposób kształtowana jest ich charakterystyka amplitudowa, co powoduje, że sygnał po przejściu przez taki układ również ulega zmianie w funkcji częstotliwości, zarówno w kwestii jego amplitudy jak i fazy. Zmiana polega na redukcji, czyli, inaczej mówiąc, na odfiltrowaniu pewnych niepożądanych składowych sygnału wejściowego – zatem filtr przepuszcza pewne częstotliwości tłumiąc inne.
W filtrach cyfrowych – choć efekt finalny jest ten sam – wygląda to zupełnie inaczej. Podczas gdy filtr analogowy działa na sygnale ciągłym, filtr cyfrowy przetwarza ciąg wartości próbek dyskretnych – a więc mamy tu do czynienia z niczym innym, jak po prostu ciągami liczb. Dlatego w przeciwieństwie do filtrów analogowych, gdzie dokonują się przemiany przebiegów prądów i napięć, w filtrze cyfrowym mamy do czynienia TYLKO z matematycznymi przekształceniami (mnożenie, dodawanie), a sam filtr cyfrowy to też nic innego jak liczby (współczynniki filtru) z zaimplementowanym algorytmem jak te współczynniki przekształcać matematycznie, aby otrzymać na wyjściu sygnał odfiltrowany cyfrowo.
Jednym ze sposobów przedstawienia filtrów FIR – tak, aby zrozumieć idee ich działania – jest porównanie ich z filtrami będącymi ich „konkurencją”, tj. filtrami o nieskończonej odpowiedzi impulsowej, czyli IIR. Ogólnie rzecz ujmując filtry typu IIR mogą być zarówno analogowe, jak i cyfrowe, „zachowujące” się tak, jak analogowe. IIR-y do uzyskania swojej odpowiedzi impulsowej potrzebują informacji „zwrotnej”, tzn. część sygnału wyjściowego trafia z powrotem na ich wejście. Takie rekurencyjne działanie filtru oznacza, iż jego odpowiedź impulsowa teoretycznie nigdy nie osiąga zera. Oczywiście w praktyce jest inaczej, bowiem sygnał wyjściowy w końcu spada do poziomu szumów. Biorąc jednak pod uwagę ten fakt (iż część sygnału wyjściowego trafia na wejście), w przypadku ich niewłaściwego zaprojektowania filtry IIR mogą być niestabilne. Wszystkie filtry analogowe są filtrami typu IIR.
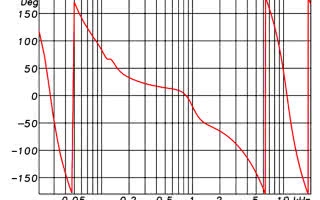
Popatrzmy jak to wygląda w praktyce. Zastosujmy tradycyjny filtr analogowy, albo filtr IIR, do skorygowania charakterystyki częstotliwościowej przykładowego głośnika – jego charakterystykę amplitudową (tego filtru) przedstawia rysunek 1a, zaś fazową 1b. Jak widać charakterystyka ta jest ograniczona od dołu i od góry pasma (mamy więc zastosowany filtr górno- i dolnoprzepustowy), a dodatkowo pomiędzy nimi mamy jakieś górki i dolinki, a nawet dolinkę w górce.

Rysunek 1. Charakterystyki częstotliwościowe przykładowego układu korygującego złożonego z filtrów typu IIR: a) amplitudowa, b) fazowa.
Każda „bulwa” w charakterystyce amplitudowej wiąże się z ujemnym (od wartości wyższych do niższych) przesunięciem fazowym, a więc zmianą na charakterystyce fazowej, zaś każda „dziura” w charakterystyce amplitudowej niesie ze sobą zmianę na charakterystyce fazowej o pozytywnym nachyleniu (od wartości niższych do wyższych). Zarówno filtracja dolnoprzepustowa, jak i górnoprzepustowa „produkują” ujemne przesunięcie fazowe. Stąd wykres zmian fazy na rysunku 1a charakteryzuje się permanentnym spadkiem (co jest związane z faktem odfiltrowania pasma w górze i dole pasma) – pamiętać bowiem trzeba, iż pionowe kreski wynikają z faktu „zawijania” charakterystyki fazowej, bowiem jest ona przedstawiana w zakresie od 180 do -180 stopni. Natomiast w części środkowej pojawiają się pewne zafalowania, odpowiadające górkom i dolinkom na charakterystyce amplitudowej.
Jak więc widać zmianom amplitudy sygnału nieodłącznie towarzyszą przesunięcia w fazie, które są nieuniknione i nieodłącznie związane z filtracją. Osoby, dla którym tematyka charakterystyki fazowej nie jest obca, są nawet w stanie przewidzieć, jak mniej więcej będzie wyglądała charakterystyka fazowa danego układu, patrząc na przebieg charakterystyki amplitudowej i vice versa. Dotyczy to jednak tylko tzw. układów minimalnofazowych, tzn. takich dla których obie charakterystyki pozostają w przewidywalnych relacjach.
Pojęcie „układu minimalnofazowego” nie oznacza bynajmniej braku przesunięć fazowych. Oznacza natomiast, iż jego charakterystyka fazowa charakteryzuje się możliwie najmniejszymi przesunięciami fazowymi towarzyszącymi zmianom charakterystyki amplitudowej. Jak wspomniałem relacje między tymi charakterystykami są przewidywalne, tak iż odpowiednie programy pomiarowe są w stanie odtworzyć przebieg jednej z tych charakterystyk na podstawie przebiegu drugiej.
Minimalnofazowość jest często bardzo pożądaną cechą filtrów. Dlaczego? Ponieważ górki i dolinki na charakterystyce amplitudowej głośnika są (przeważnie) również minimalnofazowe, jako że głośniki są (również przeważnie) układami minimalnofazowymi. Oznacza to, iż korzystając z tradycyjnych filtrów analogowych lub cyfrowych IIR (a więc minimalnofazowych) jesteśmy w stanie „naprawić” nie tylko charakterystykę amplitudową, ale również i fazową, bowiem zabiegi powodujące wygładzanie przebiegu jednej skutkują też tym samym w przypadku drugiej. Patrząc z tego punktu widzenia przesunięcia fazowe wprowadzane przez filtry nie są wcale „złem koniecznym”, ale wręcz zjawiskiem pożądanym. Dlatego też odpowiedź na pytanie „czy przesunięcie fazowe w filtrach jest dobre czy złe” – jak to przeważnie w życiu bywa – brzmi „to zależy”.
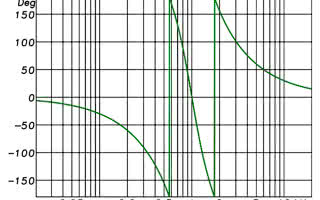
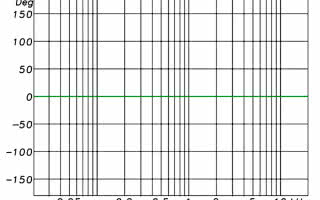
Filtry FIR mogą wprowadzać zmiany w przebiegu charakterystyki amplitudowej bez żadnych „efektów ubocznych” w postaci towarzyszących im przesunięć fazowych. Na rysunku 2 przedstawiono przebieg charakterystyki fazowej odpowiadającej charakterystyce amplitudowej z rysunku 1a – różnica polega na tym, iż filtry górno- i dolnoprzepustowy zostały zastąpione przez filtry typu FIR, dające w efekcie taki sam przebieg amplitudy sygnału, jaki uzyskaliśmy za pomocą filtru IIR (albo analogowego). Jak widać przebieg charakterystyki fazowej jest w tym przypadku linią zbliżoną do płaskiej, tzn. jej przebieg jest niezależny od częstotliwości (oprócz tych miejsc, gdzie „działają” filtry IIR, powodujące powstawanie górek i dolinek na charakterystyce amplitudowej). Stąd właśnie wzięło się określenie „liniowej fazy”, cechy charakterystycznej filtrów FIR, która pozwala dokonywać zmian amplitudy sygnału, bez żadnych zmian w fazie. Tak więc w przypadku filtrów minimalnofazowych przebiegi amplitudy i fazy są współzależne, zaś w przypadku FIR-ów są one niezależne. W filtrach FIR, patrząc na przebieg ich charakterystyki fazowej nie jesteśmy w stanie określić, jak wygląda ich charakterystyka amplitudowa – czy zastosowany filtr jest górno-, dolno- czy pasmowoprzepustowy, a może pasmowozaporowy?

Rysunek 2. Charakterystyka fazowa układu korygującego z rysunek 1, w którym filtry górno- i dolnoprzepustowy zastąpiono filtrami FIR o tej samej charakterystyce amplitudowej.
„Pozbycie” się analogowych filtrów HP i LP i zlinearyzowanie przebiegu fazy pozwoliło też lepiej widzieć, jaki wpływ na przebieg fazy mają wspomniane wcześniej podbicia i podcięcia na charakterystyce amplitudowej.
Aplikacjami, w których filtry FIR mogą się „wykazać” są crossovery. Korzystając z filtrów FIR można zaprojektować chroniący driver filtr górnoprzepustowy o niemalże dowolnym nachyleniu zbocza – wartości 96 dB/oktawę i więcej nie są tutaj niczym nadzwyczajnym.

Rysunek 3. Charakterystyki częstotliwościowe crossovera Linkwitz-Rileya 48 dB/okt. a) amplitudowa (efektem sumowania się obu charakterystyk tego typu jest idealnie płaski przebieg amplitudy), b) fazowa (suma obu filtrów).
Filtry minimalnofazowe (IIR lub analogowe) o takim nachyleniu zbocza miałyby tragiczną charakterystykę fazową. Wynika to z faktu, iż w tego typu filtrach stromym zboczom na charakterystyce amplitudowej odpowiadają równie gwałtowne zmiany przebiegu charakterystyki fazowej. Zjawisko to stawia praktyczną granicę jeśli chodzi o nachylenie (rząd) zwrotnic opartych na klasycznych filtrach. Na rysunkach 3a i 3b zaprezentowana jest charakterystyka amplitudowa i fazowa zwrotnicy IIR Linkwitz-Rileya (HP i LP) o nachyleniu 48 dB/okt. Dla porównania na rysunku 4 przedstawiona jest charakterystyka amplitudowa crossovera typu FIR 8 rzędu (o nachyleniu 96 dB/okt). Widać wyraźnie większe nachylenie zboczy filtrów crossovera. Rysunek 5 przedstawia opóźnienie grupowe (group delay) crossovera, zaś rysunek 6 jego charakterystykę fazową, po uwzględnieniu (odjęciu) opóźnienia grupowego. Jak widać charakterystyka fazowa jest idealnie płaska.

Rysunek 4. Charakterystyka amplitudowa crossovera typu FIR o nachyleniu 96 dB/okt. Efektem sumowania się obu charakterystyk jest idealnie płaski przebieg amplitudy.
Crossover z filtrami FIR pozwala nam jednocześnie „zjeść ciastko i mieć ciastko” – mamy filtry o stromych zboczach i jednocześnie liniową charakterystykę fazową. Oczywiście nie ma nic za darmo – jak widać na wykresie z rysunku 4 „płacimy” za to opóźnieniem sygnału przekraczającym 20 ms. To opóźnienie sygnału wprowadzane przez filtr FIR jest w zasadzie jedynym „hamulcowym” w powszechnym stosowaniu tego typu rozwiązań zawsze i wszędzie.

Rysunek 5. Opóźnienie grupowe zsumowanych filtrów FIR z rysunku 4.
Nas jednak, w nawiązaniu do artykułu z poprzedniego numeru, interesować będzie inne zastosowanie filtrów FIR – do korekcji charakterystyki fazowej, a także (przy okazji) amplitudowej.
Ci, którzy zajmują się pomiarami głośników, zestawów głośnikowych, a także pomieszczeń dobrze wiedzą, co to jest odpowiedź impulsowa. W teorii jest to zarejestrowana odpowiedź badanego obiektu na pobudzenie deltą Diraca, czyli impulsem o nieskończenie krótkim czasie trwania. Jak widać, już samo pojęcie „nieskończenie” uzasadnia, dlaczego jest to tylko teoria. W praktyce większość systemów pomiarowych używa przemiatanego sinusa lub sygnału typu „chip” (który jest również przemiatanym sygnałem sinusoidalnym, tylko o bardzo krótkim czasie trwania), który „przepuszcza” się przez mierzony system, a następnie rejestruje i przetwarza jego odpowiedź na charakterystykę (odpowiedź) impulsową.
Z kolei odpowiedź impulsowa może być przetransformowana w domenę częstotliwości (za pomocą FFT, a tak naprawdę DFT), co daje nam w efekcie charakterystykę amplitudową i fazową badanego systemu. Charakterystyki te natomiast mogą być przetworzone znów w domenę czasu (za pomocą odwrotnej transformaty Fouriera, czyli iFFT lub iDFT), aby uzyskać wykres odpowiedzi impulsowej systemu. Można więc prześledzić zachowanie się filtru zarówno w domenie czasowej, jak i częstotliwościowej.
Co to ma wspólnego z filtrami FIR? Odpowiedź impulsowa głośnika czy pomieszczenia jest tak naprawdę filtrem typu FIR, bowiem jej przebieg opada do 0 (lub do poziomu szumów), ze względu na jej skończoną długość. Z tego powodu filtry FIR nazywa się czasem „filtrami dziedziny czasu” lub „filtrami spotu”, pomimo tego, że w rzeczywistości ich implementacja odbywać się może poprzez mnożenie w dziedzinie częstotliwości dokonywane przez oprogramowanie lub sprzęt cyfrowy.

Rysunek 7. Charakterystyka amplitudowa głośnika (czerwona) i jej odbicie względem osi częstotliwości (zielona). Jeśli użyjemy zielonej charakterystyki jako charakterystyki filtru korygującego w efekcie otrzymamy idealną charakterystykę amplitudową (to samo tyczy się fazowej).
Jak wspomniałem odpowiedź impulsowa może być przetransformowana w dziedzinę częstotliwości i zaprezentowana w formie charakterystyk – amplitudowej i fazowej. Jeśli je odwrócimy (odbijemy względem osi częstotliwości) uzyskamy „negatyw” tych charakterystyk (rysunek 7). Jeśli przemnożymy charakterystyki oryginalne i odwrócone uzyskamy płaską linię prostą, bowiem obie te charakterystyki zniosą się wzajemnie. W dziedzinie czasu zaś otrzymamy idealny impuls.
Ma to ogromne znaczenie w pracy nad wyrównaniem charakterystyk głośnika, zestawu głośnikowego czy odpowiedzi pomieszczenia – każda zmierzona charakterystyka, po jej odwróceniu, może być zastosowana jako filtr korekcyjny. Jest to o tyle istotne, iż filtry FIR możemy projektować w dowolny sposób, tzn. można zadać nawet najbardziej „fikuśny” kształt charakterystyki amplitudowej, jak i fazowej takiego filtru. I inaczej niż w przypadku filtrów IIR, gdzie mamy określone ich typy (górno-, dolno- czy pasmowoprzepustowy, albo pasmowozaporowy) możemy zaprojektować JEDEN filtr FIR np. o charakterystyce takiej, jak ten na rysunku 8.

Rysunek 8. Charakterystykę filtru FIR możemy dowolnie kształtować, np. z wykorzystaniem zmierzonej i odbitej względem osi częstotliwości charakterystyki rzeczywistego głośnika, którą chcemy skorygować (spłaszczyć).
„Korygujące” filtry FIR można używać do:
1. Niemalże idealnego spłaszczenia przebiegu charakterystyk głośnika (zestawu czy systemu głośnikowego) – zarówno amplitudowej, jak i fazowej – włącznie z kompensacją takich anomalii, jak odbicia wewnątrz tuby drivera, wpływ grilla zestawu na wytwarzaną falę dźwiękową czy dyfrakcja na krawędziach zestawu.
2. Niwelowania anomalii pomieszczenia, takich jak efekty brzegowe w pobliżu głośnika i (bardziej w teorii niż praktyce) odbicia w pomieszczeniu.
3. Poprawy charakterystyki systemu liniowego poprzez indywidualny processing dla każdego komponentu systemu.
Charakterystykę filtru FIR można uzyskać bezpośrednio z pomiaru, odbijając ją względem osi X (osi częstotliwości) – co ciekawe dotyczy to zarówno charakterystyki amplitudowej, jak i fazowej. To, że filtr FIR może mieć liniową charakterystykę fazową nie oznacza bynajmniej, że zawsze musi ona być płaska – możemy ją równie dowolnie kształtować, jak amplitudę. Pozwalają nam na to specjalistyczne narzędzia, tj. programy, którym (wybranym) więcej uwagi poświęcimy w kolejnym numerze.
Zanim jednak do tego przystąpimy musimy sobie wyjaśnić jeszcze jedną rzecz. Filtr FIR, owszem, może zbliżyć charakterystykę naszego głośnika/zestawu głośnikowego – również pracującego w konkretnym pomieszczeniu, a więc z uwzględnieniem warunków akustycznych tam panujących – niemalże do ideału, ale w danym punkcie przestrzeni. Ponieważ nie ma dwóch punktów przestrzeni, w których odpowiedź impulsowa byłaby idealnie taka sama, nie mamy możliwości uzyskania „perfekcyjnej” korekcji dla całej nagłaśnianej przestrzeni, ani nawet dla jej większego fragmentu. Nie oznacza to bynajmniej, że korekcja FIR jest „psu na budę”, a jedynie tyle, że musimy liczyć się z tym, że nie będziemy w stanie – nawet przy wykorzystaniu najbardziej wyrafinowanych narzędzi (jak choćby wspomniany ArrayProcessing) – stworzyć przestrzeni, w której wszędzie będą panowały idealne warunki odsłuchowe. Musimy – jak to w życiu – w dalszym ciągu iść na pewne kompromisy, które będą tym większe, im większe (a więc generalnie trudniejsze) będzie pomieszczenie, które będziemy musieli nagłośnić.
Podsumujmy najistotniejsze informacje dotyczące filtrów FIR, jakie w tym artykule wysnuliśmy:
1. Filtr FIR może zmienić – nawet drastycznie – charakterystykę amplitudową głośnika czy zestawu głośnikowego, bez jakiejkolwiek zmiany jego charakterystyki fazowej. Możemy za jego pomocą zaprojektować zwrotnicę o bardzo stromych zboczach, która nie będzie wprowadzać żadnych przesunięć fazowych. Ten „bonus” niestety kosztuje – musimy liczyć się ze wzrostem latencji (opóźnienia) sygnału.
2. Każda zmierzona odpowiedź impulsowa może być użyta, jako filtr FIR. Takich możliwości korekty charakterystyk zestawów głośnikowych czy też pomieszczenia nie dawały dotychczas stosowane metody, wykorzystujące klasyczne filtry typu IIR (analogowe lub cyfrowe).
3. Filtry FIR mogą być zarówno w wersji software’owej, jak i hardware’owej, co pozwala na ich używanie do przetwarzania sygnałów w czasie rzeczywistym. Na rynku jest już kilka DSP (a także końcówek mocy wyposażonych we własne DSP), obsługujących filtry FIR zaprojektowane przez użytkownika.
Tak więc, jeśli chodzi już stricte o systemy nagłośnieniowe, filtr FIR mogą być wykorzystywane:
1. W crossoverach.
2. Do korekcji charakterystyki zestawów głośnikowych.
3. Do odsłuchiwania odpowiedzi pomieszczenia poprzez splot – czy to zmierzonej, czy wygenerowanej przez program do modelowania akustyki wnętrz.
4. Do kształtowania wiązki dźwięku w systemach typu line array.
Filtry to obecnie nie tylko „plątanina” kondensatorów, cewek i rezystorów czy też ich odpowiedniki, zrealizowane za pomocą układów scalonych. Mogą być projektowane bezpośrednio z charakterystyk lub matematycznych algorytmów i implementowane w czasie rzeczywistym z wykorzystaniem zaawansowanych technologii cyfrowego przetwarzania dźwięku.