Projektowanie filtrów FIR - korekcja charakterystyki fazowej i amplitudowej za pomocą FIR-ów (cz. III)

W tym numerze skonfrontujemy teorię z praktyką, tzn. sprawdzimy, jak nasz zaprojektowany filtr działa w rzeczywistości. Najpierw jednak przypomnijmy sobie, co już udało nam się zrobić.

PROJEKT FILTRU

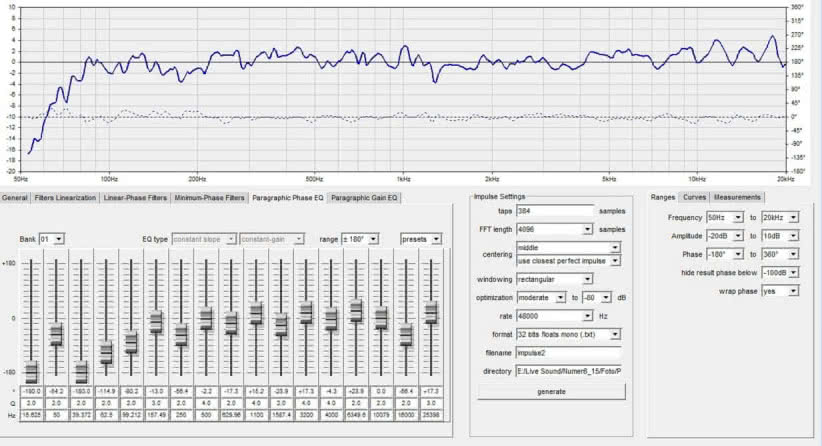
Importujemy do programu rePhase zmierzoną charakterystykę naszego zestawu głośnikowego czy też sytemu nagłośnieniowego w konkretnym pomieszczeniu (jak wiemy, pomieszczenie może w bardzo znaczący sposób wpływać na to, co tak naprawdę dotrze z nagłośnienia do uszu słuchacza znajdującego się w tym pomieszczeniu). Charakterystyka, a w zasadzie charakterystyki, bo mamy ich dwie – amplitudową i fazową – muszą być zapisane w pliku tekstowym i taki też plik jest w stanie odczytać rePhase.  Następnie, chcąc „ulepszyć” (spłaszczyć) charakterystykę amplitudową i/lub fazową korzystamy z dwóch ostatnich zakładek w oknie pod wykresem (z lewej strony ekranu) – Paragraphic Phase EQ (korekcja fazy) i Paragraphic Gain EQ (korekcja amplitudy). Są to 17-pasmowe wirtualne korektory parametryczne (paragraficzne), w których każdemu filtrowi możemy zadać dowolną wartość częstotliwości środkowej i dobroci, zaś suwakami wartość tłumienia/podbicia tego pasma (dla korektora amplitudy) lub wartość przesunięcia fazy, in plus lub in minus (dla korektora fazy). Takich 17-pasmowych banków filtrów mamy 16, tak że w sumie mamy do dyspozycji 16 x 17 czyli 272 takie pseudofiltry!
Jeśli już udało nam się osiągnąć satysfakcjonujący nas efekt w postaci docelowych charakterystyk – amplitudowej i fazowej – czas sprawdzić jak one będą wyglądały dla filtru o określonych parametrach, tj. o określonej liczbie współczynników, z odpowiednim oknem czasowym FFT i o wybranej częstotliwości próbkowania. Aby się o tym przekonać, musimy wygenerować te współczynniki. Ustawiamy odpowiednie parametry w środkowym oknie i wciskamy „generate”.

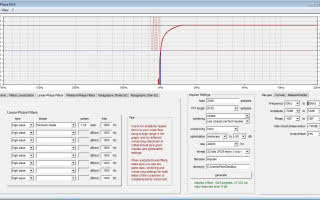
Rysunek 1. Okno filtru FIR w oprogramowaniu sterującym DSP miniSHARC firmy miniDSP – wciskając „Browse” wczytujemy z pliku .bin współczynniki filtru, a następnie przyciskiem „Send to DSP” wysyłamy je do procesora.

Po pewnym czasie – zależnym od liczby współczynników oraz wybranej optymalizacji – uzyskamy wynik w postaci pliku o wybranym przez nas formacie. Jednocześnie w okienku z domniemaną charakterystyką naszego filtru pojawiają się jego rzeczywiste charakterystyki (zarówno amplitudowa, jak i fazowa), tzn. program pokazuje nam, co przy założonych parametrach (liczbie ogniw, częstotliwości próbkowania, okienkowaniu i optymalizacji) udało się uzyskać.
W ostatnim kroku (albo ostatnim kroku tego cyklu projektowania filtru) pozostaje nam jeszcze jedno do zrobienia – skonfrontować naszą założoną charakterystykę z rzeczywistością. Jak to zrobić?

IMPLEMENTUJEMY FILTR…

Żeby zaimplementować filtr FIR, musimy przede wszystkim dysponować procesorem lub wzmacniaczem z DSP, który obsługuje tego typu filtr. Aby wczytać plik do procesora/wzmacniacza musimy go najczęściej zapisać w formie binarnej, czyli w opcji zapisu filtru wybieramy plik „.bin” – z rozwijanego okienka „Format” w sekcji „Impulse Settings” programu wybieramy wiersz „32 bits IEEE-754 mono (.bin)”. Taki plik wczytujemy następnie w odpowiednim miejscu oprogramowania procesora, który może wyglądać np. tak, jak na rysunku 1 (to akurat jest soft procesora miniSHARC firmy MiniDSP). Po wczytaniu pliku binarnego ze współczynnikami filtru ukazuje się nam jego charakterystyka amplitudowa, a – w tym konkretnym przypadku – w dolnym oknie możemy podglądnąć listę współczynników. Pamiętajmy, aby liczba współczynników zgadzała się z maksymalną liczbą, jaką może „przyjąć” nasze DSP – w przypadku mojego procesora miniSHARC jest to 2.048 współczynników. Może być ich oczywiście mniej, musimy jednak wtedy pamiętać, aby liczbę to wpisać w okienku „Taps used” na dole po prawej stronie.

Rysunek 2. Okno filtru FIR DSP wzmacniacza X4 Powersofta, obsługiwanego za pośrednictwem programu Armonia.

Teraz nie pozostaje nam już nic innego jak – znów, w tym konkretnym przypadku, przy tym oprogramowaniu – wysłać owe współczynniki do procesora (korzystając z przycisku Send to DSP) i nasz filtr jest już zaimplementowany w naszym urządzeniu. W innych DSP, z innymi programami może to wyglądać inaczej – np. w przypadku wzmacniaczy Powersofta z serii X lub K z DPS, czyli korzystając z programu Armonia, wygląda to tak, jak na rysunku 2. W tym przypadku zapisujemy współczynniki filtru w pliku tekstowym lub pliku CSV i taki importujemy do Armonii.

…I KONFRONTUJEMY Z RZECZYWISTYM POMIAREM

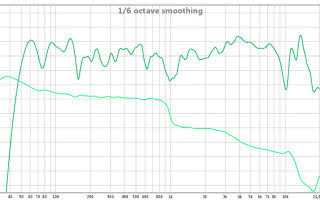
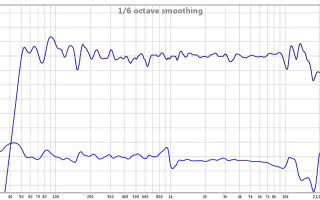
Nie pozostaje już nam nic innego, jak tylko „odpalić” system, do którego sygnał będzie „przepuszczony” przez DSP z zaimplementowanym naszym filtrem FIR i zmierzyć charakterystyki amplitudową i fazową (albo po prostu funkcję przejścia, czyli transfer function) zestawu czy systemu nagłośnieniowego. Dam głowę, że idealnej zgodności z charakterystyką, jaką wygenerował nam rePhase nie będzie, a rozbieżności będą tym większe, im mniej współczynników będzie miał nasz filtr FIR i im większy wpływ na wynik pomiaru będzie miało otoczenie, czyli np. pomieszczenie, w którym będziemy mierzyć nasz system (idealnie byłoby dokonać pomiaru w komorze bezechowej). W naszym przypadku wygląda to tak, jak pokazują wykresy na rysunkach 3, 4, 5 i 6. Pierwszy z nich pokazuje wczytaną do rePhase charakterystykę zestawu, który będziemy „naprawiać” – widać, że charakterystyka amplitudowa, choć niezła, daleka jest od ideału, a faza zmienia się dość mocno (wykres odwiniętej fazy, linią przerywaną, wędruje od ok. 670 stopni do ponad -720 stopni!). Rysunek 4 prezentuje planowaną (grantowa) i domniemaną, tj. wygenerowaną przez program (czerwona) charakterystykę zestawu głośnikowego „potraktowanego” naszym filtrem FIR o 2.048 współczynnikach i częstotliwości próbkowania 48 kHz. Jak widać latencja jest dość spora, bo wynosi ponad 21 ms, a ponadto w zakresie najniższych częstotliwości pojawiły się zafalowania, dość znacznie odbiegające od naszej założonej linii prostej.

Rysunek 3. Wczytana do rePhase charakterystyka zestawu, który będziemy „naprawiać” – faza kiepska, zmienia się od ok. 670 stopni do ponad minus 720 stopni.

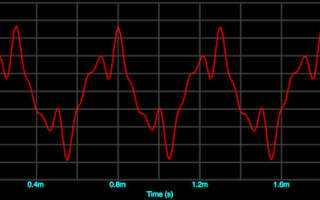
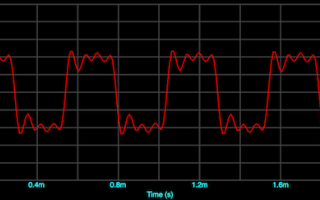
Z kolei rysunek 5 pokazuje jeszcze raz jak wyglądała zmierzona charakterystyka (amplitudowa i fazowa) naszego zestawu przed korekcją filtrem FIR, zaś na rysunku 6 – po aktywacji filtru FIR. Widać, jak ładnie udało nam się zlinearyzować charakterystykę fazową, a i na polu poprawy charakterystyki amplitudowej osiągnęliśmy znaczące sukcesy. Niektóre głębokie wcięcia pozostały i nasze zabiegi nie pomogły – bo też pomóc nie mogły, gdyż są to obszary nieminimalnofazowe, czyli takie, których korekcją nie poprawimy (wynikają z sumowania się fali bezpośredniej i odbitej, np. od ściany czy podłogi, która dla tej częstotliwości jest w przeciwfazie z falą bezpośrednią) – np. w okolicy 77,5 Hz, 155 Hz czy 630 Hz. Oczywiście można jeszcze bardziej dopieszczać charakterystykę, wszak wirtualnych filtrów mamy 272, czyli praktycznie każdą, nawet najmniejszą górkę i dolinkę można wyrównać. To, czy gra jest warta świeczki, czy nie, to inna rzecz – czy takie „zasypanie” 1-decybelowych dolinek, czy „ścinanie” pagórków da jakiś wymierny efekt odsłuchowy czy nie, pozostawiam do rozważenia każdemu z osobna.Nie ulega natomiast wątpliwości, że mocno „pogięta” charakterystyka fazowa ma wpływ na odtwarzanie, szczególnie transjentów – co ilustruje rysunek 7, gdzie na lewym wykresie mamy przedstawiony przebieg prostokątny o częstotliwości 2 kHz odtwarzany przez zestaw głośnikowy przed skorygowaniem jego charakterystyki fazowej, zaś po prawej po korekcji. Różnica, jak widać, jest istotna. Podobnie „naprawienie” fazy można zauważyć przyglądając się charakterystykom impulsowym. Na rysunku 8 – znów – na górze odpowiedź impulsowa układu z „pozawijaną” fazą, a na dole z fazą spłaszczoną.Na koniec jeszcze – choć naszym przewodnim tematem jest poprawa charakterystyki danego systemu/zestawu nagłośnieniowego – kilka słów o drugim sposobie projektowanie filtru FIR.

Rysunek 4. Planowana (grantowa) i rzeczywista, wygenerowana przez program (czerwona) charakterystyka zestawu głośnikowego „potraktowanego” filtrem FIR o 2.048 współczynnikach i częstotliwości próbkowania 48 kHz.

TWORZYMY CROSSOVER O PŁASKIEJ FAZIE

Możemy stworzyć filtr FIR od zera, tzn. nie importując żadnej charakterystyki, a kształtując charakterystykę amplitudową i fazową (w sposób zależny, jak i niezależny) filtru poczynając od płaskiego przebiegu ich obu. Charakterystyki owe możemy kształtować bądź korzystając z wirtualnych filtrów paragraficznych fazy i amplitudy, bądź też – jeśli projektujemy crossover – z gotowych presetów filtrów dolno- i górnoprzepustowych również kilku różnych typów (zarówno o zmiennej, jak i niezmiennej fazie). Program rePhase daje nam kilka możliwości, jeśli chcemy stworzyć swój cyfrowy crossover. Tu również mamy dwie możliwości – albo tworzymy sam crossover, który będzie w pewien sposób elastyczny, albo projektujemy nasz crossover pod konkretny zestaw głośnikowy, mając wcześniej zmierzone charakterystyki tych głośników w ich pełnym paśmie pracy (a więc bez żadnych filtrów czy zwrotnic). Sposób drugi jest niejako połączeniem tego, o czym mówiliśmy sobie przed momentem oraz w poprzednim odcinku – możemy w ten sposób zarówno zaprojektować dla niego odpowiedni crossover, jak i popracować nad charakterystykami.

Jeśli tworzymy crossover „uniwersalny”, a więc nie bazujemy na zmierzonej charakterystyce głośnika, będziemy korzystać z jednej z dwóch zakładek – Linear-Phase Filters i Minimum-Phase Filters. W tym drugim przypadku możemy zaprojektować zwykły crossover minimalnofazowy, a więc taki, w którym zmianom amplitudy sygnału (filtracji dolno- lub górnoprzepustowej) będą towarzyszyły adekwatne zmiany fazy – np. filtr Butterwotha II rzędu przesuwa fazę o 180 stopni, a IV rzędu (24 dB/okt.) o 360 stopni. W zakładce możemy wybierać między filtrami Butterwortha i Linkwitza-Rileya, o regulowanym nachyleniu charakterystyki z krokiem co 6 dB/okt (nawet do 996 dB/okt!!), oraz filtry I i II rzędu (a więc o nachyleniu – odpowiednio – 6 i 12 dB/okt), przy czym ten drugi o regulowanym parametrze Q, dzięki czemu możemy z niego stworzyć filtr Butterwortha, Bessla, Czebyszewa i inne. Nas jednak bardziej będzie interesowała druga zakładka – wszak do stworzenia „zwykłych” crossoverów nie potrzebujemy tak zaawansowanych narzędzi, jak DSP obsługujące filtr FIR. Po to przecież chcemy użyć FIR-a (godząc się na wszelkie z tym związane niedogodności, jak np. zwiększona latencja), aby mieć możliwie najbardziej płaską fazę. To właśnie uzyskamy korzystając z filtrów o liniowej fazie (Linear-Phase Filters). Tutaj także znajdziemy najprostsze filtry, a więc I i II rzędu (w tym drugim również możemy regulować dobroć Q) oraz Linkwitza-Rileya – ale teraz, niezależnie od tego jak bardzo stromy filtr wybierzemy, faza pozostanie cały czas niezmieniona. Oprócz tych „klasyków” znajdziemy tu jeszcze filtry „zakładkowe” (overlapping) o wybieranej szerokości pasm zachodzących na siebie w sąsiadujących ze sobą filtrach górno- i dolnoprzepustowym (1/2, 1, 2 i 3 oktawy), strome filtry odcinające dolne i górne pasmo częstotliwości (rysunek 9), mało znane filtry Horbacha-Keele’a (rysunek 10) oraz filtr typu „Brickwall” (ceglany mur), który w swojej idealnej wersji charakteryzuje się nieskończenie dużym nachyleniem zbocza zaczynającego się dokładnie w punkcie odcięcia filtru (rysunek 11, wykres granatowy). Oczywiście fizycznie filtry te są w takiej postaci nierealizowalne – na rysunku 11 czerwoną linią przedstawiona jest realna charakterystyka amplitudowa filtru Brickwall o 2.048 współczynnikach. Nawet zwiększając liczbę tych współczynników do „kosmicznej” wartości 8.182 (popatrzcie, jaka wtedy jest latencja przy 48 kHz – 85 ms!) – abstrahując oczywiście od tego, czy jakieś DSP byłoby w stanie przyjąć filtr o takiej liczbie współczynników – jeszcze do ideału trochę brakuje, choć już jest dużo bliżej, niż przy 2.048 współczynnikach (rysunek 12).

Rysunek 12. Filtr Brickwall o 8.182 współczynnikach (latencja przy 48 kHz ponad 85 ms!!).

To chyba „z grubsza” tyle, jeśli chodzi o projektowanie filtrów FIR za pomocą darmowego oprogramowania rePhase. Za miesiąc przyjrzymy się innym narzędziom do tego służącym – również darmowym, jak i tym, za które trzeba co nieco zapłacić.