X4L - wzmacniacz z DSP z serii X
Biznes „nagłośnieniowy” – w porównaniu z innymi dziedzinami techniki (np. przemysłem samochodowym, czy ...
Po wstępnie teoretycznym dotyczącym filtrów cyfrowych w ogólności, a w szczególności filtrów typu FIR, w tym numerze przejdziemy już do konkretów, czyli do tego, jak zaprojektować taki filtr przy użyciu kilku różnych – w większości darmowych – programów. Rozpoczniemy od rePhase, który – pomimo tego, że jest za darmo – oferuje naprawdę sporo możliwości.
Korzystając z rePhase można stworzyć filtr cyfrowy o skończonej odpowiedzi impulsowej na dwa sposoby – można to zrobić „od zera” lub wykorzystując do tego zmierzoną już charakterystykę, którą dzięki naszemu filtrowi będziemy chcieli poprawić. W tym drugim przypadku „naprawiać” możemy zarówno przebieg amplitudy, jak i fazy i to – co, jak wiemy jest duża zaletą FIR-ów – zupełnie niezależnie. Z racji tego, że naszym tematem jest korekcja charakterystyki fazowej i amplitudowej za pomocą FIR-ów zajmiemy się szczegółowym omówieniem tej drugiej opcji.
Żeby mieć co „poprawiać” musimy najpierw dysponować charakterystyką – amplitudową i fazową, czyli inaczej funkcją przejścia (transfer function) – zestawu lub systemu głośnikowego (bądź też pojedynczego głośnika), który weźmiemy „na warsztat”. Pomiary głośników/zestawów głośnikowych to osobny temat, mam jednak nadzieję, że ktoś, kto będzie chciał brać się za dość poważny temat, jakim jest projektowanie korekcyjnych filtrów FIR, odpowiednią wiedzę na ten temat posiada. Kiedy już zmierzymy nasz zestaw/system nagłośnieniowy, otrzymaną charakterystykę musimy wyeksportować (zapisać) w trybie tekstowym (.txt). Tak zapisany plik po wyedytowaniu w dowolnym edytorze tekstowym wygląda mniej więcej tak, jak (we fragmencie) rysunek 1. Taki plik można następnie zaimportować do programu rePhase, korzystając z rozwijanego menu File/Import Measurement. Przykład takiej charakterystyki zestawu, który będziemy próbować korygować naszym filtrem FIR, przestawia rysunek 2 – jest to zrzut ekranowy z programu rePhase po zaimportowaniu owej charakterystyki, na którym grubszą linią ciągłą uwidoczniono przebieg charakterystyki amplitudowej, a przerywaną charakterystyki fazowej.

Rysunek 1. Fragment pliku tekstowego z wyeksportowaną charakterystyką amplitudową i fazową zestawu głośnikowego.
Chcąc „ulepszyć” charakterystykę amplitudową i/lub fazową korzystamy z dwóch ostatnich zakładek w oknie pod wykresem (z lewej strony ekranu) – Paragraphic Phase EQ (korekcja fazy) i Paragraphic Gain EQ (korekcja amplitudy). Są to 17-pasmowe korektory parametryczne (paragraficzne), w których każdemu filtrowi możemy zadać dowolną wartość częstotliwości środkowej i dobroci, zaś suwakami wartość tłumienia/podbicia tego pasma (dla korektora amplitudy) lub wartość przesunięcia fazy, in plus lub in minus (dla korektora fazy). Co ciekawe nie jesteśmy „skazani” tylko na jedną wartość zakresu zmian amplitudy czy fazy – możemy wybrać zakresy od ±3 dB do ±96 dB(!) dla amplitudy oraz od ±10º do ±720 º!
To nie koniec „atrakcji”, bowiem takich 17-pasmowych banków filtrów mamy 16, tak że gdy wykorzystamy wszystkie 17 filtrów pierwszego banku, przechodzimy do następnego i znów możemy użyć kolejnych 17 filtrów, równolegle do banku poprzedniego, i tak aż do ostatniego banku. W sumie więc mamy do dyspozycji 16 x 17 czyli 272 w pełni parametryczne filtry. Mało tego, każdy bank może mieć inne zakresy pracy filtrów, tak więc w jednym banku możemy dokonać zgrubnej korekcji filtrami o szerokim zakresie wzmocnienia/tłumienia czy zmian fazy, a następnie filtrami w innym banku „dopieścić” jeszcze bardziej przebieg charakterystyk, za pomocą precyzyjnych filtrów o małym zakresie pracy.

Rysunek 2. Zaimportowane do programu rePhase charakterystyki z pliku tekstowego z rysunku 1.
Mamy też możliwość wyboru rodzaju filtru (dotyczy to tylko korekcji amplitudy), przy czym do wyboru mamy filtry półkowe (low i high), typu constant Q i proportional Q, filtry o stałym nachyleniu (constant slope) i stałym kształcie (constant shape) oraz filtry cosinusowe (rised cosine), a poza tym możemy wybrać, czy mają to być filtry minimalnofazowe (w których zmianie amplitudy towarzyszy proporcjonalna zmiana fazy) czy filtry o liniowej fazie (faza nie ulega zmianie przy zmianie amplitudy) – nie dotyczy to filtrów cosinusowych i filtrów o stałym nachyleniu, które z definicji są filtrami o liniowej fazie. Oczywiście tak naprawdę nie są to żadne filtry, sensu stricte, ale pasma o wybieranej szerokości (dobroci), które możemy regulować w zakresie zmian amplitudy i/lub fazy. Reasumując, mamy więc 272 takie pasma, które pozwalają na niemalże dowolne dostrajanie zaimportowanej charakterystyki, osobno dla fazy i amplitudy.
Gwoli ścisłości – będąc już przy temacie, co „potrafi” program rePhase – dodam jeszcze, że możemy też stworzyć swój filtr FIR od zera, tzn. nie importując żadnej charakterystyki, a kształtując charakterystykę amplitudową i fazową (w sposób zależny, jak i niezależny) filtru poczynając od płaskiego przebiegu ich obu. Charakterystyki owe możemy kształtować bądź korzystając z wirtualnych filtrów paragraficznych fazy i amplitudy, bądź też – jeśli projektujemy crossover – z gotowych presetów filtrów dolno- i górnoprzepustowych, również kilku różnych typów (zarówno o zmiennej, jak i niezmiennej fazie).
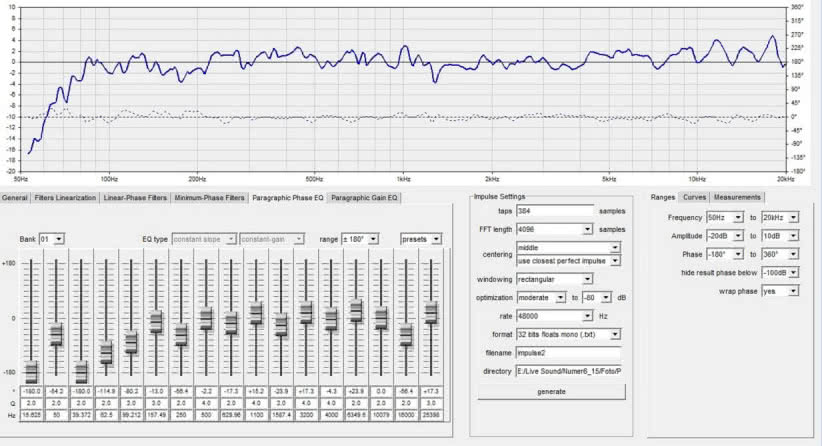
Mając zaimportowaną charakterystykę, którą chcemy poprawić – tzn. możliwie najlepiej ją zlinearyzować (amplitudową i fazową) – możemy przystąpić do „zabawy” suwaczkami naszych wirtualnych filtrów w zakładkach Paragraphic Phase EQ i Paragraphic Gain EQ. Powiedzmy, że udało nam się osiągnąć satysfakcjonujący nas efekt w postaci docelowych charakterystyk – amplitudowej i fazowej – które mogą na przykład wyglądać tak, jak te z rysunku 3 (zarówno na rysunku 3a, jak i 3b są te same charakterystyki, natomiast pokazane zostały dwa razy, aby uwidocznić, w jaki sposób – jakimi wirtualnymi filtrami i o jakich parametrach – taki efekt udało się uzyskać). Jak widać z rysunków 3a i 3b domniemany efekt udało się uzyskać „zatrudniając” do tego tylko 16 najprostszych filtrów typu constant Q korygujących amplitudę i 13 korygujących fazę. Czy aby na pewno nam się to udało?

Rysunek 3a. Pracując mozolnie suwakami wirtualnych korektorów amplitudy i fazy udało nam się uzyskać satysfakcjonując nas efekt: a) pod charakterystykami parametry filtrów użytych do linearyzacji fazy, b) filtry użyte do linearyzacji charakterystyki amplitudowej.
Jak widać w środkowym okienku pod wykresem, sąsiadującym z oknem z suwakami wirtualnych filtrów, zaryzykowaliśmy zaprojektowanie filtru 37. rzędu (pierwsze okienko od góry), a więc o 37 współczynnikach (samplach) – lepiej będzie to widoczne w zbliżeniu, na rysunku 4. Wiadomo (mam nadzieję), iż im większy rząd filtry FIR (im więcej współczynników), tym większa rozdzielczość w dziedzinie częstotliwości, co ma szczególnie istotne znaczenie w zakresie niższych częstotliwości. Wiadomo też (również mam nadzieję), że im więcej współczynników, tym większa latencja wprowadzana przez filtr – co wynika z liczby mnożeń wykonywanych przez procesor DSP, potrzebnych do uzyskania efektu filtracji sygnału. Czy więc 37 ogniw (współczynników) filtru wystarczy, aby uzyskać charakterystykę, jak na rysunku 3?

Rysunek 4. W sekcji środkowej pod wykresem ustalamy parametry naszego filtru FIR – m.in. jego rząd (liczbę współczynników), częstotliwość próbkowania, optymalizację, okno czasowe i format zapisu danych filtra. Na dole informacja o jego latencji.
Aby się o tym przekonać, musimy wygenerować te współczynniki. Oprócz rzędu filtru możemy wybrać też długość słowa FFT (co znów wpływa nam na rozdzielczość, tym razem konwersji odpowiedzi impulsowej filtru na jego charakterystyki częstotliwościowe) oraz rodzaj okna czasowego (duży wybór, ale tym parametrem nie musimy sobie zbytnio zawracać głowy, zostawiając domyślne prostokątne, czyli rectangular, albo trójkątne (triangular) lub Blackmana-Harrisa. Optymalizację najlepiej zostawić domyślną, czyli średnią (moderate), istotne natomiast będą dwa kolejne okienka. W pierwszym wybieramy częstotliwość próbkowania filtru, co będzie miało swoje skutki w postaci różnych wartości latencji oraz rozdzielczości. Im większa częstotliwość próbkowania, tym mniejsza latencja, która zawsze równa się połowie liczby współczynników (w naszym przypadku 18, bowiem wszystkich współczynników jest 37). Czas trwania jednego sampla jest jednak uzależniony od częstotliwości próbkowania – im ona jest wyższa, tym ten czas jest krótszy, a więc i latencja będzie mniejsza. Np. dla częstotliwości próbkowania 44,1 kHz czas trwania jednej próbki wynosi ok. 22,5 mikrosekundy, a więc latencja naszego filtru 37. rzędu wyniesie ok. 0,4 milisekundy (18 x 22,5 μs = 0,4 ms). Nie musimy tego zresztą wcale liczyć – wielkość latencji wprowadzanej przez nasz filtr widzimy na samym dole okienka z parametrami filtru, w postaci liczby sampli i czasu w milisekundach. Tak nawiasem mówiąc, możemy tam też zobaczyć, jaka będzie maksymalna wartość amplitudy charakterystyki naszego filtru, w stosunku do referencyjnej wartości 0 dB.
Jeśli jednak ustawimy dużą częstotliwość próbkowania, przy małej liczbie ogniw filtru jego rozdzielczość będzie bardzo marna (zaraz to pokażemy). Drugi istotny parametr do ustawienia to format danych o naszym filtrze. Możemy uzyskać nasz filtr w formie pliku WAV (jest to odpowiedź impulsowa naszego filtru, czyli po prostu wartość poszczególnych próbek/współczynników filtru). I tutaj mamy do wyboru 16- 24- i 32-bitowe pliki w formacie LPCM (linear PCM), jak i 32-bitowym IEEE, w obu przypadku zarówno w trybie mono, jak i stereo. Możemy też nasze współczynniki uzyskać w formie pliku binarnego (32 bity IEE-745 mono), a także – co nas będzie najbardziej interesowało – w postaci pliku tekstowego (również 32-bitowy filtr mono). Są jeszcze dwa pliki w postaci zmiennoprzecinkowych tablic. Na koniec pozostaje nam wybrać nazwę dla naszego pliku z danymi o filtrze oraz destynację, w której będzie on zapisany, a na koniec nacisnąć przycisk „generate”.

Rysunek 5. Po wciśnięciu przycisku „generate” program pokazuje nam, co udaje się uzyskać z charakterystyką wyjściową „potraktowaną” naszym filtrem FIR, przy założonych parametrach (liczba ogniw filtra 37, częst. próbkowania 44,1 kHz – wykres czerwony).
Po pewnym czasie – zależnym od liczby współczynników oraz wybranej optymalizacji – uzyskamy wynik w postaci pliku o wybranym przez nas formacie. Jednocześnie w okienku z domniemaną charakterystyką naszego filtru pojawiają się jego rzeczywiste charakterystyki (zarówno amplitudowa, jak i fazowa), tzn. program pokaże nam, co udaje się uzyskać przy założonych parametrach (liczbie ogniw, częstotliwości próbkowania, okienkowaniu i optymalizacji). Wygląda to tak, jak na rysunku 5. Widać, iż o ile w zakresie wysokich częstotliwości uzyskaliśmy dużą zgodność wykresu założonego i wynikowego, o tyle w zakresie niższym do naszego ideału (wykres niebieski) trochę nam brakuje, a w przypadku fazy również i w zakresie środka. No cóż, latencja nieprzekraczająca pół milisekundy przy częstotliwości próbkowania 44,1 kHz to żadna latencja, możemy więc nieco „zaszaleć” i spróbować np. stworzyć filtr 1.000. rzędu. Wpisujemy więc w pierwszym okienku liczbę tysiąc (automatycznie długość słowa FFT wzrasta nam do 8.192). No to „generate”! I jak?

Rysunek 6. Zwiększając liczbę współczynników (rząd) filtru do 1.000 uzyskujemy dużo większą zbieżność charakterystyki założonej z wynikową, zwiększa nam się za to dość istotnie latencja.
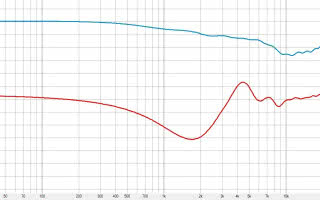
Noooo, od razu widać dużą poprawę, wykresy uzyskują bardzo dużą zbieżność, i to praktycznie w całym zakresie użytecznym (rysunek 6). Faza również przepiękna. Gdzie tkwi haczyk? Ano, latencja wzrosła nam już do ponad 11 ms, co nie jest już takie niezauważalne. To prawie 4 metry różnicy w dystansie, czyli tak, jakbyśmy odsunęli się od naszego źródła dźwięku o kilka kroków – tragedii jeszcze nie ma, ale w przypadku odsłuchu na słuchawkach (np. w systemach IEM) byłbym już ostrożny. Przy częstotliwości próbkowania 48 kHz w dalszym ciągu przebieg charakterystyk jest mocno zbieżny, ale też i latencja jakoś szczególnie nie zmalała – ot, tylko do ok. 10,5 ms. Jeśli jednak „szarpniemy” się na 96 kHz, to o ile latencja wyniesie już tylko nieco ponad 5 ms, o tyle charakterystyki w dole pasma znów zaczynają się nam rozjeżdżać, choć dopiero poniżej 150 Hz (rysunek 7). Jeszcze gorzej wygląda owe 96 kHz przy naszym 37-rzędowym filtrze FIR – tutaj charakterystyki nam się rozjeżdżają już poniżej 6 kHz!

Rysunek 7. Dla filtru 1.000. rzędu i częstotliwości próbkowania 96 kHz latencja znów spada – do nieco ponad 5 ms – jednak charakterystyki w dole pasma znów zaczynają się rozjeżdżać.
Widać więc, jak ostrożnie trzeba dobierać parametry i nie szafować nimi zbyt hojnie (jak mam, to czemu nie użyć), bowiem po pierwsze filtr może okazać się po prostu niepraktyczny (np. o zbyt dużej latencji), albo daleko odbiegający od ideału (zbyt duża częstotliwość próbkowania w stosunku do liczby ogniw filtru). Po drugie zaś trzeba też liczyć się z ograniczeniem sprzętowym procesora DSP, który nasz filtr będzie „przeżuwał” – przeważnie zarówno maksymalna liczba ogniw filtru, jak i częstotliwość próbkowania są z góry narzucone. Dla przykładu DSP wzmacniaczy Powersofta X4 i X8 ma ograniczoną maksymalną liczbę współczynników filtru do 384, a częstotliwość próbkowania musi wynosić 48 kHz.

Rysunek 8. Poddając analizie częstotliwościowej plik WAV z odpowiedzią impulsową (współczynnikami) filtru FIR otrzymujemy jego charakterystykę w funkcji częstotliwości – zarówno amplitudową (niebieska), jak i fazową (czerwona).
Możemy także zobaczyć, jak wygląda charakterystyka samego filtru, który zaprojektowaliśmy (a nie jak być może będzie wyglądała charakterystyka naszego urządzenia, po przepuszczeniu sygnału doń docierającego przez nasz filtr). Wystarczy w ostatnim okienku (na dole po prawej) w zakładce Measurements wcisnąć „bypass”. Wtedy właśnie zamiast charakterystyki wynikowej, możemy zobaczyć charakterystyki (amplitudową i fazową) naszego filtru, zarówno tego idealnego (niebieska), jak i tego, jaki jesteśmy w stanie uzyskać przy założonych parametrach. Oczywiście można też sobie zapisać nasz filtr w pliku WAV, a następnie poddać go analizie w innym programie FFT – wynik czego przedstawia rysunek 8. Jednak program rePhase też to umożliwia, bez konieczności eksportowania, importowania i analizowania plików – wystarczy wcisnąć jeden przycisk i mamy to jak na dłoni (rysunek 9). Widać, że przebieg charakterystyki amplitudowej jest odzwierciedleniem suwaków naszego wirtualnego korektora paragraficznego, a przy 1.000 współczynników i częstotliwości próbkowania 44,1 kHz (latencja 11,34 ms) mamy tylko niewielką rozbieżność w stosunku do charakterystyki „idealnej” w okolicy 120 i 190 Hz, nieprzekraczającą 1 dB. Z kolei na rysunku 10 widać, jak niewielka jest rozdzielczość w zakresie niskich częstotliwości filtru 37. rzędu, gdzie założona przez nas 4-decybelowa „górka” w okolicy 62 Hz jest całkowicie „niewidzialna” dla filtru, podobnie jak próby zmiany fazy w okolicach 100 Hz.

Rysunek 10. Na tych wykresach widać, jak niewielka jest rozdzielczość w zakresie niskich częstotliwości filtru 37. rzędu – założona przez nas „górka” w okolicy 62 Hz jest całkowicie „niewidzialna” dla filtru, podobnie jak próby zmiany fazy w okolicach 100 Hz.
Jeśli ktoś myśli, że to koniec pracy to się myli. To dopiero połowa sukcesu – teraz trzeba skonfrontować to z rzeczywistością. Ale o tym już w kolejnym wydaniu LSI.