Faza i opóźnienie grupowe

To jednak tylko „półprawda”, bowiem aby mieć pełen obraz tego jak zachowuje się nasze badane urządzenie, powinniśmy znać nie tylko zmiany amplitudy sygnału (czyli charakterystykę amplitudową), ale również jego fazy (charakterystykę fazową). Mamy wtedy kompletny zestaw informacji, ot np. taki, jak na rysunku 1, gdzie na wykresie górnym mamy pierwszą, a na dolnym drugą z wymienionych charakterystyk.

Przeważnie ignorowana charakterystyka fazowa – często z braku jakiejkolwiek wiedzy na temat, co tak naprawdę przedstawia i jak to się ma do rzeczywistych właściwości urządzenia – dostarcza nam wielu istotnych informacji o tym, czy badane urządzenie jest wysokiej klasy, czy zaprojektowane „po łebkach”, i czego można spodziewać się po nim, tzn. jaki będzie efekt finalny jego „pracy”. Na przykład w przypadku urządzeń głośnikowych będzie to dla nas już pewną informacją, jakiej spodziewać się wierności odtwarzanego sygnału trafiającego na jego wejście. Może się bowiem okazać, iż dwa głośniki o niemalże identycznej charakterystyce amplitudowej będą grały ze słyszalną różnicą – co może wyjaśnić odmienny przebieg charakterystyki fazowej jednego i drugiego głośnika.

CHARAKTERYSTYKA FAZOWA

Przyjrzyjmy się więc bliżej charakterystyce fazowej i ogólnie fazie sygnału.

Sygnał przechodzący przez jakikolwiek system podlega opóźnieniu – niezależnie od tego, czy będzie to system analogowy, czy cyfrowy, i czy będzie to układ akustyczno-mechaniczno-elektryczny, czy też urządzenie czysto elektroniczne. Oczywiście możemy się spodziewać, że analogowe urządzenie elektroniczne będzie charakteryzować się najmniejszym opóźnieniem, rzędu nanosekund, a może i mniej, fakt jest jednak faktem, że ZAWSZE to opóźnienie wystąpi.

Opóźnienie to może być niezależne od częstotliwości („czysty” delay), ale może też być zależne częstotliwościowo. Z tym pierwszym przypadkiem mamy do czynienia np. w systemach cyfrowych, które charakteryzują się pewnym, mierzonym w mikrosekundach czy też milisekundach opóźnieniem propagacji sygnału (latencją), ale też i w systemach analogowych, jeśli rozważamy system akustyczny jako całość (np. czas dotarcia sygnału od źródła do mikrofonu, spowodowany określoną odległością między nimi i również określoną prędkością rozchodzenia się fal dźwiękowych). Z drugim przypadkiem – opóźnieniem zależnym od częstotliwości – będziemy mieć do czynienia, jeśli faza sygnału będzie różna dla różnych częstotliwości.

Co to takiego jest ta faza?

Faza to nie to samo, co polaryzacja. Często opisując znany wszystkim realizatorom przycisk w kanale wejściowym konsolety używamy określanie „odwrócenie fazy”, co jest błędem (żeby nie powiedzieć, nonsensem). Faza sygnału występuje zawsze względem jakiegoś sygnału odniesienia i jest ona zarówno względna, jak i całkowicie biegunowa. Dodatnie ciśnienie na membranie mikrofonu, które skutkuje wychyleniem membrany głośnika do przodu (w stronę słuchacza) oznacza, że system jest, z absolutnego punktu widzenia, spolaryzowany dodatnio (pozytywnie). Jeśli membrany w dwóch głośnikach wychylają się równocześnie w przód (i równocześnie w tył), są wzajemnie spolaryzowane dodatnio, niezależnie od swoich polaryzacji absolutnych. Odwrotna polaryzacja odwraca przebieg czasowy sygnału równo dla wszystkich częstotliwości. Faza nie może więc być „dodatnia”, czy „pozytywna”, „ujemna” bądź „negatywna”, ani też „odwrócona”. Może być tylko „przesunięta” w czasie względem sygnału referencyjnego. Przesunięcie fazy (fazowe) skutkuje późniejszym przybyciem sygnału w stosunku do sygnału referencyjnego.

Znając przesunięcie fazowe sygnału dla danej częstotliwości (w stopniach) możemy obliczyć opóźnienie tegoż sygnału (również dla tej częstotliwości) w sekundach lub metrach – jeśli przeliczymy je sobie na odległość, przyjmując jakąś określoną wartość prędkości dźwięku, która też przecież nie jest zawsze taka sama w każdym warunkach.

Wzór na przeliczenie czasu na częstotliwość to oczywiście:

T = 1/f

gdzie:
T – czas w sekundach
f – częstotliwość w Hz

Przykładowo więc, jeśli dla 100 Hz mamy przesunięcie fazowe sygnału (w stosunku do jakiegoś sygnału referencyjnego) o 90 stopni (co, jak mam nadzieję wiemy, stanowi ¼ długości fali), to będzie ono odpowiadało opóźnieniu o 2,5 ms (długość fali dla 100 Hz to 1/100 Hz, czyli 0,01 s, a ¼ z tego to 0,0025 s, czyli 2,5 ms). Jeśli przesunięcie fazy nie jest tak „jednoznaczne”, tzn. nie wynosi 45, 90 czy 180 stopni, ale np. 13°, bardzo łatwo możemy policzyć, jaka to będzie część długości fali – dzieląc ową wartość przesunięcia przez 360° (to jest tyle, ile wynosi pełny okres), a potem już jak w przykładzie powyżej. A więc dla naszego przykładu z częstotliwością 100 Hz będzie to wyglądało tak:

13°/360° = 0,0361
1/100 Hz = 0,01 s
0,01 s x 0,0361 = 0,000361 s = 0,361 ms (albo 361 μs)

Ok, dość matematyki, wróćmy do naszej charakterystyki fazowej.

Opóźnienie sygnału możemy więc przedstawić zarówno jako wykres amplitudy sygnału w funkcji czasu (charakterystyka impulsowa – rysunek 2) albo też jako wykres zmian fazy w funkcji częstotliwości (rysunek 3) lub wykres zmian opóźnienia grupowego (group delay) w funkcji częstotliwości (rysunek 4).

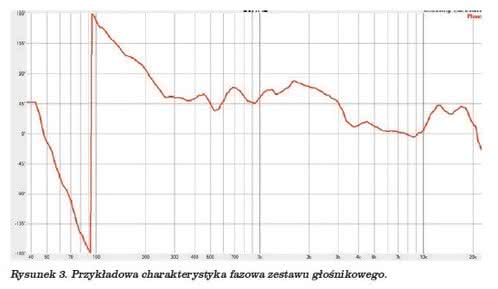
Te dwa ostatnie wykresy są tożsame, prezentując te same informacje, tylko w inny sposób (przed chwilą przeliczaliśmy żmudnie przesunięcie fazy na opóźnienie – na wykresach mamy to podane „na patelni”, dla wszystkich częstotliwości).

Jeśli chcemy zanalizować charakterystykę fazową jakiegoś urządzenia, powinniśmy najpierw pozbyć się stałego w funkcji częstotliwości („czystego”) opóźnienia sygnału, spowodowanego czasem dotarcia sygnału od źródła do mikrofonu i latencją systemu pomiarowego, pozostawiając tylko opóźnienie, które wynika z przetworzenia sygnału przez nasze urządzenie (np. głośnik czy system nagłośnieniowy). Opóźnienie to możemy „zaaplikować” urządzeniu pomiarowemu, przy czym najczęściej używanymi obecnie narzędziami są programy komputerowe do analizy sygnału (typu SMAART, SatLive, SysTune itp.), które same potrafią obliczyć wartość tego opóźnienia i zadać go w programie.

JAK WYGLĄDA CHARAKTERYSTYKA FAZOWA

Co dzieje się z charakterystyką fazową, jeśli nie uwzględnimy w analizatorze wartości stałego opóźnienia? Będziemy mieć wtedy sytuację, w której sygnał z mierzonego urządzenia będzie opóźniony w stosunku do sygnału referencyjnego, co spowoduje powstanie tzw. efektu filtra grzebieniowego. Charakterystyka fazowa będzie wtedy opadająca linią prostą o stałym nachyleniu – jeśli oś częstotliwości będzie liniowa (rysunek 5).

W przypadku gdy oś częstotliwości wyskalujemy logarytmicznie – tak jak przeważnie robi się to dla charakterystyk częstotliwościowych – będziemy mieli do czynienia z wykresem opadającym…logarytmicznie (rysunek 6).

Z uwagi jednak na to, że przeważnie zakres wartości osi Y wynosi od -180° do 180° (lub od 0° do -360°), w momencie gdy przesunięcie fazowe osiągnie wartość -180°, nastąpi „zawinięcie” wykresu – „przeskoczy” on do góry, do wartości 180 stopni, aby móc dalej podążać ku wartościom coraz mniejszym. I tak do momentu, aż znów osiągniemy -180°, itd., itd. Stąd na wykresie proste pionowe linie, pomiędzy którymi mamy linie opadające logarytmicznie. Gdybyśmy „odwinęli” fazę, tzn. nie ograniczali się tylko do zakresu od -180° do 180°, to faza sygnału opóźnionego w stosunku do referencyjnego o 5 ms wyglądała by tak, jak na rysunku 7. Ot i cała tajemnica „poszatkowanej” często charakterystyki fazowej.

Widać więc, iż jeśli nie pozbędziemy się stałego opóźnienia, odczytanie właściwej charakterystyki fazowej – czyli tej „części”, która jest zależna od częstotliwości – jest mocno utrudnione.

Wartość stałego opóźnienia, wynikającego z propagacji sygnału, możemy odczytać bądź z charakterystyki impulsowej, bądź charakterystyki opóźnienia grupowego. W pierwszym przypadku wystarczy spojrzeć na skalę czasową i odczytać w którym miejscu wypada najwyższa wartość impulsu. W przypadku charakterystyki opóźnienia grupowego opóźnienie stałe odczytamy na osi Y – odpowiada ona tej wartości czasu, gdzie wykres opóźnienia grupowego przyjmuje stałą wartość (wykres przebiega równolegle do osi X). Możemy – na upartego – odczytać to opóźnienie również z charakterystyki fazowej, z tym że tutaj już nie mamy tego podanego „na tacy”, ale musimy troszkę policzyć. Odczytujemy, dla jakiej wartości częstotliwości następuje pierwsze „zawinięcie” fazy – czyli gdzie przesunięcie fazowe osiąga -180°, co odpowiadać będzie połowie fali – i ze wzoru T = 1/2f obliczamy czas opóźnienia. W naszym przykładzie (z rysunku 5 i 6) faza zawija się po raz pierwszy przy 500 Hz, czyli 1/(2·500 Hz) = 1/1.000 Hz = 0,001 s = 1 ms – a więc wszystko się zgadza.

Spójrzmy jeszcze, na przykładzie, co się stanie, jeśli niedokładnie odczytamy ten czas opóźnienia propagacji sygnału, który musimy uwzględnić w programie, aby uzyskać „czysty” wykres przebiegu fazy.

Przypadek, gdy odejmiemy „za mało” niczym w zasadzie nie różni się od przypadku, gdy w ogóle nie uwzględnimy tego, że mamy stałą latencję sygnału. Tzn. różni się – wartością tegoż opóźnienia, co oznaczać będzie, że charakterystyka fazowa będzie wtedy „gęściejsza” (zawijanie fazy będzie znacznie częściej, bowiem czas opóźnienia będzie krótszy niż w sytuacji, gdy w ogóle go nie uwzględnimy), a wykres opóźnienia grupowego istotnie zbliży się do osi X (aczkolwiek będzie wciąż nad nią, właśnie o te kilka milisekund, czy nawet mikrosekund, o które pomyliliśmy się w naszych kalkulacjach). Sytuację to ilustruje rysunek 8, gdzie mamy – od góry patrząc – charakterystykę impulsową, fazową i opóźnienia grupowego przykładowego zestawu głośnikowego, gdzie uwzględniono nieco mniejsze opóźnienie sygnału propagacji niż jest w rzeczywistości – 1,917 ms zamiast 2,917 ms (stąd impuls przesunięty o 1 ms w prawo, a wykres opóźnienia grupowego 1 ms nad osią X).

Co się natomiast stanie, jeśli przesadzimy w naszych kalkulacjach i wpiszemy zbyt duży czas propagacji, większy niż w rzeczywistości?

ZA DUŻO

W tym przypadku będziemy mieli dziwną sytuacje, gdy wykres opóźnienia grupowego przejdzie poniżej osi X, czyli opóźnienie będzie miało wartość ujemną. W sytuacji absolutnej takie coś nie może się wydarzyć (nie możemy mieć ujemnego opóźnienia, bo to by oznaczało, że sygnał dociera szybciej niż „po drucie”, tzn. musiałby się poruszać szybciej niż prędkość światła!). Jednak musimy pamiętać, że w naszym przypadku nie mamy do czynienia z czasem absolutnym, ale relatywnym – w stosunku do innego sygnału, referencyjnego – stąd ujemny czas opóźnienia. Również charakterystyka fazowa wygląda wtedy dość „dziwnie” – pomiędzy pionowymi kreskami zawijania fazy wykres nie opada, ale wznosi się (rysunek 9). Tak więc jeden rzut oka, czy to na charakterystykę opóźnienia grupowego, czy też charakterystykę fazową, powinien nam wystarczyć, aby zorientować się, że „coś jest nie w porządku”, tzn. że uwzględniono w kalkulacjach latencję większą niż jest w rzeczywistości.

CZAS OPÓŹNIENIA IDEALNIE DOBRANY

W przypadku gdy dobrze skalkulujemy czas opóźnienia, uzyskamy „prawdziwy” przebieg charakterystyki fazowej, a charakterystyka opóźnienia grupowego „przyklei” się do osi X (rysunek 10).

Teraz wreszcie można przyjrzeć się jak wygląda przebieg fazy sygnału mierzonego, tzn. które częstotliwości „nie nadążają” i w jakim stopniu. Czas zadać pytanie

DLACZEGO JEST TO TAKIE ISTOTNE?

Płaska charakterystyka amplitudowa i fazowa pozwalają urządzeniu wiernie odtwarzać sygnał, który trafia na jego wejście. Najchętniej stosowanymi sygnałami testowymi, pozwalającymi określić jakość urządzenia – pod względem wierności przekazu – są sygnał impulsowy i fala prostokątna, oba charakteryzujące się bardzo szerokim widmem. W praktyce wszystkie urządzenia audio mają ograniczony zakres pracy (ograniczone pasmo przenoszenia), są bowiem elementami pasmowo- przepustowymi. Z definicji więc nie mogą idealnie wiernie reprodukować sygnałów, nawet tych mieszczących się z zakresie częstotliwości słyszalnych dla ludzkiego ucha.

Zarówno charakterystyka amplitudowa, jak i fazowa są interesujące dla projektanta systemów głośnikowych jako narzędzie pozwalające mu na osiągnięcie jak najlepszego przenoszenia transjentów przez ów system. Mogą one dostarczyć ilościowej oceny charakterystyki głośnika, uzależnionej od doboru komponentów i ich umiejscowienia. Zupełnie słusznie oczekuje się, że lepsze przenoszenie transjentów przekłada się na wierniejszą reprodukcję dźwięku, co jest pożądaną cechą systemów nagłośnieniowych.

W praktyce charakterystyka opóźnienia grupowego wykorzystywana jest do wyrównywania czasowego poszczególnych komponentów wielodrożnego systemu głośnikowego – czy to przetworników w zestawie głośnikowych, czy też składników całego systemu dźwiękowego, np. subbasów z „górkami”. Charakterystyka fazowa natomiast może być wykorzystywana do zbadania, czy szczyty i dolinki na charakterystyce amplitudowej powiązana są z „działalnością” minimalnofazowych filtrów korekcyjnych.

 

URZĄDZENIE MINIMALNOFAZOWE

Dla danej charakterystyki amplitudowej istnieje nieskończona liczba charakterystyk fazowych, które mogą jej odpowiadać. Dzieje się tak dlatego, że charakterystyka amplitudowa jest „ślepa czasowo”, tzn. nie zawiera żadnych informacji dotyczących czasowych/fazowych zależności między poszczególnymi częściami spektrum.

Filtry pasmowe (a do takich też zalicza się głośnik) zawsze wprowadzają przesunięcie fazowe sygnału. Charakterystyką minimalnofazową jest taka, która wykazuje najmniejsze przesunięcie fazy dla danego przebiegu charakterystyki amplitudowej. Można ją wyznaczyć, za pomocą transformaty Hilberta, z charakterystyki amplitudowej. Ma ona płaski przebieg charakterystyki fazowej w tych zakresach, gdzie charakterystyka amplitudowa jest również płaska.

URZĄDZENIE NIE-MINIMALNOFAZOWE

Choć pożądanym jest, aby urządzenie głośnikowe było minimalnofazowe, nierzadko spotykamy takie zestawy, które niestety nie są minimalnofazowe. Oznacza to, że charakterystyka amplitudowa takiego urządzenia może być płaska, podczas gdy charakterystyka fazowa „zawija się”, tzn. charakteryzuje się większym odchyleniem niż 180 stopni. Przeważnie wynika to z zastosowania zwrotnicy wyższego rzędu i nie skompensowania jej wpływu na sygnał. Powoduje to „nieczasowe” (nie w tym samym czasie) sumowanie się sygnałów ze współpracujących ze sobą głośników, co skutkuje słyszalnymi efektami np. w postaci „chowania” się części pasma. Generalnie wszyscy są zgodni co do tego, że wykazywanie przez urządzenie charakterystyki minimalnofazowej skutkuje poprawą jakości przetwarzania urządzenia. Co w takim razie można zrobić, aby ten warunek spełnić?

ROZWIĄZANIE

Istnieje kilka sposobów na uzyskanie charakterystyki minimalnofazowej w urządzeniach czy systemach wielodrożnych. Jedną z nich jest zastosowanie w zwrotnicach filtrów Buttherwortha I rzędu. Pozwala to uzyskać charakterystykę minimalnofazową, jednak nachylenie 6 dB/oktawę jest często zbyt małe, aby zapewnić skuteczną ochronę driverów przed sygnałem spoza ich pasma pracy.

Drugim sposobem jest stosowanie filtrów cyfrowych FIR. Mogą one modyfikować charakterystykę amplitudową bez wpływania na fazę sygnału. Ceną, jaką musimy za to zapłacić, jest zwiększona latencja układu – tym większa, im niższej z częstotliwością chcemy zejść.

Trzecie rozwiązanie to stosowanie filtrów wszechprzepustowych do skorygowania nieminimalnofazowej charakterystyki urządzenia. Na ten temat już jakiś czas temu ukazał się na łamach LSI (wtedy jeszcze LSP) artykuł Johna Murraya. Zaletą tego rozwiązania jest uzyskanie charakterystyki minimalnofazowej z wykorzystaniem filtrów IIR, co pozwala utrzymać latencję na niskim poziomie oraz skorzystać z filtrów o odpowiednio dużym nachyleniu do ochrony drivera.

Piotr Sadłoń