
X4L - wzmacniacz z DSP z serii X
Biznes „nagłośnieniowy” – w porównaniu z innymi dziedzinami techniki (np. przemysłem samochodowym, czy ...

Niejednokrotnie zastanawialiście się zapewne, jak to jest tak naprawdę z tą „cyfrą”? Każdy, niewątpliwie, orientuje się jakie zalety i wady ma praca w dziedzinie cyfrowego przetwarzania dźwięku. Bezspornym faktem jest to, że w dzisiejszych czasach dokonanie i „obrobienie” zupełnie przyzwoicie brzmiących nagrań jest dostępne dla „zwykłego śmiertelnika”, dysponującego przeciętnym komputerem z przeciętną kartą muzyczną, kilkoma dobrymi mikrofonami, mikserkiem i jeszcze paroma drobiazgami (no i przede wszystkim dobrym słuchem oraz pewnymi umiejętnościami, czego jednakże za żadne pieniądze kupić się nie da). Również w dziedzinie nagłośnienia coraz mniej jest zagorzałych wrogów konsolet cyfrowych, a już chyba nikt nie kręci nosem na fakt, że w raku znajduje się kilka procesorów, które w 99% przypadków są przecież urządzeniami cyfrowymi.
Zasadniczo ludzie dzielą się na dwa rodzaje: tych, którym do szczęścia wystarczy sam fakt, że coś jest, i ewentualnie wiedza jak się tym posługiwać, oraz drugą grupę, tych co lubią rozkręcać, dociekać i „kminić” co, z czym, gdzie, jak i dlaczego. Właśnie do owej drugiej grupy jest kierowany ten cykl, dotyczący tego, co ma jakikolwiek związek z dźwiękiem cyfrowym. Będziemy starali się przedstawić wszystkie aspekty tego tematu, począwszy od samego początku, czyli przetwarzania A/C i C/A, powiemy też trochę o kodowaniu, przetwarzaniu (DFT, FFT), filtracji cyfrowej, nie może zabraknąć też tematu cyfrowej transmisji dźwięku, aczkolwiek znaczną część tego tematu (sieci cyfrowe) już poruszyliśmy w ostatnich numerach LSP. Postaram się nie zalać czytelnika mnóstwem wzorów i definicji, typu: „...z usprawiedliwionym zastosowaniem własności jednorodności...” czy „...w takiej sytuacji W(f) ? 0 ? f...”, ale też będę starał się w miarę rzetelnie omówić poszczególne tematy i zagadnienia. Zacząć jednak musimy, jak to w życiu, od podstaw.
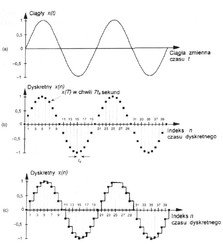
Rysunek 1. Przebieg sinusoidalny w dziedzinie czasu: a) reprezentacja przebiegu o czasie ciągłym (sygnał analogowy), b) dyskretna reprezentacja próbkowa (sygnał o czasie dyskretnym), c) skwantowana reprezentacja sygnału (sygnał cyfrowy).
Na czym polega różnica między sygnałem analogowym a cyfrowym? Skąd się wzięły te nazwy? Otóż sygnał analogowy jest odwzorowaniem przebiegu zmian parametrów fizycznych (ciśnienia, prędkości akustycznej) przez sygnał elektryczny (napięcie, natężenie prądu). Nazwa „sygnał analogowy” wzięła się stąd, iż w zamierzchłych czasach (tzn. gdy jeszcze duchem Adolfa straszono małe dzieci), kiedy jeszcze nie istniały komputery cyfrowe, wszelkie obliczenia wykonywały maszyny wielkości szafy trzydrzwiowej, zbudowane z setek lamp elektronowych, a potem tranzystorów i diod. Wszelkie operacje wykonywały układy różniczkująco-całkujące, połączone ze sobą za pomocą staromodnych kabli połączeniowych, używanych w telekomunikacji. W taki sposób ciągłe napięcie lub prąd w rzeczywistym obwodzie były analogowe do pewnej zmiennej w równaniu różniczkowym, takiej jak prędkość, temperatura, ciśnienie powietrza, itp. Sygnał analogowy jest więc określony w każdej chwili czasu i może przyjmować dowolne wartości w danym zakresie. Dlatego też nazywany jest często sygnałem ciągłym (Rysunek 1a).
Następnym krokiem w kierunku „cyfryzacji” sygnału jest proces próbkowania sygnału. Więcej na ten temat w kolejnym artykule, teraz wystarczy nam to, że próbkowanie polega na zmierzeniu i zapamiętaniu wartości sygnału analogowego w określonych chwilach czasu (Rysunek 1b). W dalszym ciągu sygnał taki może przybierać dowolne wartości, ale jest określony tylko w tych konkretnych chwilach czasowych, których umiejscowienie na osi czasu jest zależne od częstotliwości próbkowania. Otrzymujemy więc sygnał zwany w literaturze sygnałem o czasie dyskretnym (nie chodzi tu o dochowanie tajemnicy, ale właśnie o fakt określenia wartości sygnału tylko w pewnych „dyskretnych” punktach osi czasu). Taki sygnał nie nadaje się jednak do tego, aby procesor mógł go „strawić”. Musimy dokonać również operacji kwantyzacji, która spowoduje, że wartość sygnału przybierze również określone wartości (Rysunek 1c). Oznacza to, że dopuszczamy tu do powstawania pewnego błędu w przetwarzaniu, który możemy minimalizować przez zmniejszenie szerokości przedziałów kwantowania (czyli zmniejszeniu wysokości „schodków”), jednakże nigdy nie uda nam się zlikwidować go całkowicie. Więcej o tym również powiemy sobie w jednym z następnych artykułów.
A więc jest, nasz upragniony, długo oczekiwany, najprawdziwszy z prawdziwych sygnał cyfrowy! I cóż się okazuje? O ile sygnał analogowy był przebiegiem, z obserwacji którego (przy odrobienie umiejętności i znajomości tematu) możemy określić pewne cechy tego sygnału, o tyle sygnał cyfrowy to po prosty nudny, monotonny ciąg cyfr, i to w dodatku w kodzie dwójkowym, dla normalnego Europejczyka równie wymownym, jak „Baśnie tysiąca i jednej nocy” w oryginalnej wersji językowej (dla niewtajemniczonych – po arabsku). W ten prosty sposób doszliśmy dlaczego tak trudno dogadać się człowiekowi z komputerem. On po prostu „myśli” w zupełnie innym języku (swoją drogą, o wiele łatwiejszym od ludzkiego, bo obejmującym tylko dwa znaki – ale o tym za moment). Żeby jednak komputer nie robił nas w przysłowiowego „balona”, trzeba choć z grubsza poznać jego język, który choć złożony tylko z dwóch elementów – „0” i „1” – może przysporzyć komuś niemało siwych włosów. Symbole „0” i „1” odpowiadają po prostu różnym poziomom napięć, np. „0” odpowiada napięciom w zakresie 0-0,8 V, „1” odpowiada np. napięciom w granicach 4-5 V.
Podstawowymi zaletami zmiennych binarnych są:
– łatwość ich generowania
– pewność transmisji
– łatwość ich zapamiętywania
– prostota układów realizujących operacje logiczne i arytmetyczne na zmiennych binarnych.
Otaczający nas świat jest jednak opisany zmiennymi o znacznie bardziej złożonej strukturze aniżeli zmienne binarne, musimy zatem symbole przedstawiające te zmienne kodować za pomocą uporządkowanych zbiorów symboli zer i jedynek.
Chodzi oczywiście o kody, ten ludzki i ten komputerowy. Kod dziesiętny składa się z 10 cyfr, od 0 do 9. Jeśli „idziemy” od 0 wzwyż dochodzimy do 9 i wskakuje nam znowu 0, a na pozycję wyżej 1, jako pierwsza dziesiątka. I tak dalej aż do 99, i znowu te pozycje nam się zerują, a pojawia 1 przed nimi jako określenie setek, potem tysięcy, milionów itd. Z kodem binarnym jest podobnie, z tym że tam ten przyrost kolejnych pozycji „w górę” odbywa się o wiele szybciej. Kiedy po zerze pojawi się jedynka zaraz potem zeruje nam się ona a „wskakuje” jedynka „oczko wyżej” i tak dalej. Może przykład, będzie łatwiej. Rozpiszmy sobie jak się ma pierwsze 15 cyfr kodu dziesiętnego do binarnego:

Widać więc, że w zależności od ilości pozycji w kodzie binarnym możemy określić ile liczb kodu binarnego nam się ”zmieści”. W przypadku czterech pozycji możemy opisać 16 cyfr (od 0 do 15), dla pięciu pozycji już 32, dla ośmiu – 256, a dla szesnastu – 65.536, itd.
Pojedynczy znak binarny nazywa się bitem. Osiem bitów tworzy bajt (ang. byte). Pomiędzy tym jest jeszcze ciąg czteroelementowy, czasami zwany kęsem BCD. I dalej, szesnaście bitów tworzy słowo 16-bitowe, 32 – słowo 32-bitowe, itd. Strukturę słowa 8-bitowego, czyli bajtu, pokazuje Rysunek 2. Bit a0 nosi nazwę bitu najmniej znaczącego i oznacza się go skrótem LSB (ang. Least Significant Bit). Bit o największym indeksie, czyli pierwsze od lewej, nosi nazwę bitu najbardziej znaczącego i oznacza się go skrótem MSB (ang. Most Significant Bit). Duże zbiory informacji byłyby mało czytelne, gdyby trzeba było powiedzieć, że plik dźwiękowy ma rozmiar 684752158 bajtów. Dlatego, jak w normalnym życiu, stosuje się przedrostki: kilo (k), mega (M) i giga (G), z tym że 1 kilobajt to nie 1.000 bajtów, ale 1024 (210 bajta). Tak samo przedrostek mega nie oznacza 1.000.000 ale 1024*1024, czyli 1.048.576, no i giga to 1024*1024*1024 (kto ciekawy, niech sobie przeliczy, ile to wychodzi).

Rysunek 2. Struktura słowa 8-bitowego, czyli bajtu. Bit a0 nosi nazwę bitu najmniej znaczącego (LSB). Bit o największym indeksie nosi nazwę bitu najbardziej znaczącego (MSB).
Przedstawiony tu kod binarny nazywany jest kodem binarnym prostym. Istnieją jeszcze pewne odmiany kodów binarnych, każdy bazujący tylko na ciągu „0” i „1”, ale sposób ich organizacji w całym ciągu jest różny dla różnych kodów. Są to np. kody dwójkowo-dziesiętne (kody BCD – ang. Binary Coded Decimal), kod uzupełnień do dwóch (U2 – najbardziej rozpowszechniony w operacjach arytmetycznych), kod Graya. Mamy też kody detekcyjne, służące do wykrywania przekłamań i błędów transmisji, oraz kody korekcyjne, do zadań których należy naprawianie tychże błędów, aby na wyjściu otrzymać prawidłowy, niezniekształcony sygnał cyfrowy. Nie będziemy jednak sobie nimi głowy zawracać, bo to już wyższa szkoła jazdy, do niczego nam zupełnie niepotrzebna w naszej codziennej pracy realizatorów.
Pod tym tajemniczym hasłem kryje się kilka zdań na temat formatu danych numerycznych (wiem, że niektórzy z was w tej chwili podejmują decyzję, aby odpuścić sobie dalszą lekturę tego artykułu, ale proszę jeszcze o gram cierpliwości. Często spotkać można w literaturze sformułowanie typu: „...wyposażony w procesor operujący na danych zmiennoprzecinkowych...” lub coś w tym stylu, warto więc wiedzieć, co to za „żaba” i jak ją połknąć). Rozróżniamy następujące formaty danych numerycznych:
Liczby stałoprzecinkowe (stałopozycyjne). Istotą tego formatu jest umownie ustalone (tzn. istniejące tylko w świadomości programisty) położenie przecinka między bitami „całości” a „ułamków”.
Zaletami liczb stałoprzecinkowych są:
– duża szybkość realizacji operacji arytmetycznych
– duża łatwość konwersji kodu
– duża dokładność przedstawiania liczby dziesiętnej
– powszechność stosowania tego formatu w układach wejść i wyjść analogowych
Wadą liczb stałoprzecinkowych jest:
– konieczność aktualizacji i wyrównania współczynników skalowych,
– konieczność korekcji przepełnienia arytmetycznego
Zdając sobie sprawę z tego, że ostatnie dwa punkty zasadniczo są równie pasjonujące, jak zestawienie rocznej produkcji roślin motylkowych na białostocczyźnie (z całym szacunkiem dla tego pięknego regionu), nie będę rozwijał tego tematu. Poprzestańmy na tym, że są to dość kłopotliwe uciążliwości, które spowodowały, że w bardziej zaawansowanych systemach stosuje się
Liczby zmiennoprzecinkowe. Liczba taka składa się z dwóch liczb binarnych:
– K-bitowego ułamka M, zwanego mantysą
– L-bitowej liczby całkowitej W, będącej wykładnikiem potęgowym. Odpowiada jej liczba dziesiętna X = M * 2W.
Dużą zaletą liczb zmiennoprzecinkowych jest radykalne uproszczenie programowania w stosunku do liczb stałoprzecinkowych. Do wad należy zaliczyć mniejszą dokładność przedstawiania liczby dziesiętnej oraz mniejszą szybkość operacji arytmetycznych.
Myślę, że jak na początek, to i tak spora dawka „ciężkiej” wiedzy, tak więc w tym artykule to by było na tyle. Zainteresowanych tematyką i wytrwałych zapraszam za dwa miesiące, będzie mowa o znacznie ciekawszych, a co ważniejsze praktycznych, tematach, tj. próbkowaniu, kwantowaniu oraz błędach i problemach z nich wynikających.
Jan Erhard
