
X4L - wzmacniacz z DSP z serii X
Biznes „nagłośnieniowy” – w porównaniu z innymi dziedzinami techniki (np. przemysłem samochodowym, czy ...
Jak pamiętamy z artykułu o próbkowaniu, mamy już sygnał, który ma pewne wartości w określonych chwilach czasu. Jednakże sygnał taki może w dalszym ciągu przyjmować nieskończenie wiele wartości z danego zakresu, czyli trudno byłoby go nam opisać za pomocą sygnału cyfrowego, który ma skończony zbiór wartości, jakie może przyjmować.
Trzeba więc nasz spróbkowany sygnał przyporządkować do jednego z przedziałów kwantowania, na które zostaje podzielony pełny zakres przetwarzania. Pomówimy więc w tym artykule o
Już na samym wstępie trzeba powiedzieć, iż o ile – przynajmniej w teorii – próbkowanie było procesem w pełni odwracalnym, o tyle kwantowanie już z definicji takowym nie jest. W wyniku tego procesu powstaje bowiem błąd, ponieważ pewnej liczbie x(n) na wyjściu konwertera odpowiada wiele wartości z przedziału x1 ±q/2 (q – wielkość przedziału kwantowania). Najwcześniejszą i do niedawna najpopularniejszą metodą kwantowania była zaproponowana przez Widrowa metoda kwantowania równomiernego, popularnie zwana modulacją kodowo-impulsową (PCM). Polega ona na podzieleniu całego zakresu, w jakim może zmieniać się sygnał wejściowy, na k równomiernie rozłożonych przedziałów kwantowania o stałych szerokościach (rysunek 1). Jeśli n bitów jest przeznaczonych do reprezentowania każdej wartości próbki, wtedy całkowita liczba reprezentowanych wartości sygnału wynosi:

zaś zakres dynamiczny, wyrażony w mierze logarytmicznej, określa zależność:

Widzimy więc, że kwantowanie „degraduje” sygnał na tyle, że nie jest możliwa jego idealna rekonstrukcja. Sygnał skwantowany przybiera postać schodkową, co powoduje pojawienie się wyższych harmonicznych w sygnale, które teoretycznie powinny być usunięte w procesie rekonstrukcji. W praktyce jest tak, że składowe te tworzą produkty intermodulacji, będące źródłem zniekształceń nieliniowych. Ogólnie błędy kwantyzacji mogą być zamodelowane jako źródło szumu dodawanego do sygnału. Dla przyjętego modelu szumu wzór na stosunek sygnału do szumu S/N przybiera postać:

Zależność jest powszechnie stosowana do określania teoretycznego zakresu dynamiki konwertera PCM.

Istotną sprawą jest fakt, że wielkość zniekształceń zależy w znacznym stopniu od stosunku bieżącego poziomu sygnału do maksymalnego zakresu przetwarzania. Dla przykładu, dla kwantyzera 16-bitowego (n=16, czyli zakres przetwarzania 97,8 dB) sygnał o poziomie -80 dB względem poziomu maksymalnego spowoduje powstawanie zniekształceń równych ok. 1,5 %. Jest to zrozumiałe, jeśli zauważymy, że przy dużym zakresie konwertera i wykorzystaniu tylko kilku procent tego zakresu mamy do czynienia z takim samym przypadkiem, jak byśmy przetwarzali ten sam sygnał, ale w konwerterze dajmy na to 6 bitowym. Oczywiste jest, że przy mniejszej liczbie bitów (a więc i przedziałów kwantowania) szerokość tych przedziałów jest o wiele większa, a więc i dokładność przetwarzania maleje. Należy dążyć do możliwie największego wysterowania przetwornika A/C, czyli takiej sytuacji, gdy maksymalna wartość sygnału „zajmuje” prawie cały zakres przetwornika.

Równie niewskazanym, jak niedosterowanie, a nawet jeszcze mniej przyjemnym zjawiskiem, jest przesterowanie przetwornika, tj. podanie takiego sygnału, który byłby większy od maksymalnego zakresy przetwarzania. W przeciwieństwie do przesterowania urządzenia analogowego, gdzie niewielkie przesterowanie jest w praktyce niesłyszalne lub słabo słyszalne, nawet niewielkie przekroczenie zakresu maksymalnego spowoduje wygenerowanie sygnału, który może niewiele mieć wspólnego z tym faktycznym na wejściu (w „analogu” będzie to sygnał co prawda zniekształcony, ale wciąż skorelowany z oryginałem).
Stosuje się dwa sposoby kwantowania, czyli przyporządkowania wartości rzeczywistych sygnału wartościom dyskretnym: poprzez zaokrąglanie lub poprzez obcinanie. Najczęściej stosowaną operacją, umożliwiającą zapis liczb na skończonej ilości bitów, jest zaokrąglanie. Polega ono na wyborze najbliższego poziomu kwantowania według zasady matematycznej: x 0,5 – zaokrąglenie „w górę”, x = 0,5 – zaokrąglenie do liczby parzystej (rysunek 2a). W drugim przypadku mamy do czynienia z operacją obcinania najmłodszego bitu (rysunek 2b). Wzrost szumów spowodowany zaokrąglaniem i obcinaniem liczb można traktować podobnie jak szum kwantyzacji.
W sytuacji gdy mamy do czynienia z większymi częstotliwościami próbkowania i dużą rozdzielczością bitową (np. 24 bity), tradycyjna metoda PCM nie sprawdza się zbyt dobrze. W takim przypadku możemy skorzystać z innych metod, do których należy metoda różnicowa. Głównym założeniem jej jest to, że kwantyzacji poddaje się nie bezpośrednio wartości próbek, lecz różnicę pomiędzy dwiema kolejnymi próbkami. Pozwala to na ograniczenie liczby bitów potrzebnych do zapisania sygnału bez dużych zniekształceń i błędów. Jest to możliwe dzięki zaobserwowaniu zjawiska polegającego na tym, że składowe widmowe sygnału audio o małych częstotliwościach (które przenoszą znaczną cześć energii sygnałów), choć mogą mieć dużą amplitudę, to jednak ich pochodna jest bardzo mała. Co to dla nas oznacza? Ano to, że składowe te charakteryzują się wolno narastającymi i opadającymi zboczami.
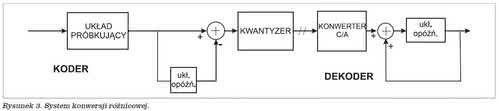
Rysunek 3 przedstawia schemat ideowy systemu konwersji różnicowej (koder razem z dekoderem). W koderze, po układzie próbkującym mamy urządzenie dokonujące odejmowania próbki bieżącej i opóźnionej, a następnie kwantyzator tej różnicy. Sygnał po kwantyzacji jest zamieniany na postać analogową i dodawany do poprzedniej wartości sygnału. Dzięki kwantyzacji różnicowej następuje dość znaczna poprawa stosunku sygnał/szum, jednakże należy ograniczyć jej stosowanie do sygnałów, w których dominują składowe widma o niższych częstotliwościach (w przypadku np. dźwięków perkusyjnych dokładność kwantyzera różnicowego może nie być zadowalająca). Zwiększając częstotliwość próbkowania zmniejszamy błąd, gdyż maleje nam krok kwantyzacji, a dzięki temu amplituda sygnału w poszczególnych krokach kwantyzacji nie zmienia się zbyt gwałtownie.
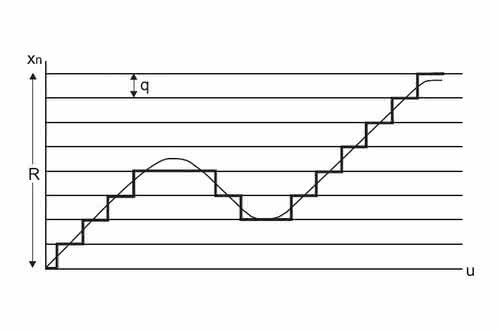
Konwersja jednobitowa, zwana również konwersją delta, przypomina nieco różnicową, z tym że w tym przypadku nie dokonujemy kwantyzacji różnicy pomiędzy kolejnymi próbkami. W konwersji jednobitowej ta różnica jest stała i może wynosić +1 albo -1. Sygnał analogowy jest w tym przypadku zamieniany na ciąg próbek, z częstotliwością znacznie przekraczającą częstotliwość Nyquista. W każdym okresie próbkowania jest obliczany sygnał błędu – w przypadku gdy jest on dodatni, impuls jest dodawany do sygnału, w sytuacji gdy błąd jest ujemny – odejmowany. Dzięki temu uzyskujemy schodkową aproksymację sygnału analogowego, jak na przykład pokazuje rysunek 4.

Błędy pojawiające się w procesie konwersji jednobitowej mogą być dwojakiego typu. Pierwszy z nich to błąd nienadążania. Powstaje on w przypadku gwałtownych zmian sygnału wejściowego, kiedy konwerter nie jest w stanie nadążyć za takimi zmianami sygnału. Wynika to z tego, że wartość poszczególnych „schodków” jest stała, a więc i maksymalna szybkość narastania sygnału aproksymującego ma określoną wartość.

Drugi błąd pojawia się w sytuacji odwrotnej, tj. wtedy gdy sygnał przez pewien okres czasu przyjmuje mniej więcej stałą wartość (lub gdy nie ma sygnału, czyli ma on wartość 0). Błąd ten nazywamy szumem granulacyjnym, gdyż sygnał wyjściowy oscyluje wokół sygnału oryginalnego, zmieniając swój stan z 1 na 0, z 0 na 1, itd. Ponieważ szum wynikający z gwałtownych zmian sygnału jest skorelowany z sygnałem wejściowym, jest on mniej dokuczliwy dla słuchacza, niż szum granulacyjny o tym samym poziomie. Ilustracja powyższych błędów jest zaprezentowania na rysunku 5. W tym artykule to by było na tyle. W kolejnym numerze przejdziemy do konkretów, tzn. do przetworników analogowo-cyfrowych, oraz spróbujemy odpowiedzieć sobie na pytanie, jak unikać lub minimalizować te błędy i zniekształcenia przetwarzania, o których przeczytaliśmy w tym i poprzednim artykule.
Jan Erhard
Autor z wykształcenia jest informatykiem i specjalistą od sieci cyfrowych, zaś z zamiłowania muzykiem. Zajmuje się też realizacją dźwięku, stąd jego zainteresowania i duża wiedza na temat cyfrowego przetwarzania sygnałów.
